values = seq(-10,10,length.out = 100)
density = dnorm(values)
plot(density)
3 Posterior estimation
In the previous chapter, we have calculated our posterior distribution by multiplying prior and likelihood across a set of possible values, and then dividing by the sum of all those to standardize (this is the p(D) in the Bayesian formula). In all but the most simple models, this technique will not work.
The reason is the so-called “curse of dimensionality” - imagine we have a statistical model with 20 parameters. Imagine we would say for each of this 20 parameters, we consider 20 possible values to evaluate the shape of the posterior - the number of values we would have to calculate would be
\[ n = 20^{20} \approx 10^{26} \] which is probably larger than the memory of your computer. Thus, we need another way to calculate the shape of the posterior. The main method to do this in Bayesian inference is MCMC sampling.
3.1 What is an MCMC?
A Markov-Chain Monte-Carlo algorithm (MCMC) is an algorithm that jumps around in a density function (the so-called target function), in such a way that the probability to be at each point of the function is proportional to the target. To give you a simple example, let’s say we wouldn’t know how the normal distribution looks like. What you would then probably usually do is to calculate a value of the normal for a number of data points
To produce the same picture with an MCMC sampler, we will use teh BayesianTools package. Here the code to sample from a normal distribution:
library(BayesianTools)
density = function(x) dnorm(x, log = T)
setup = createBayesianSetup(density, lower = -10, upper = 10)
out = runMCMC(setup, settings = list(iterations = 1000), sampler = "Metropolis")BT runMCMC: trying to find optimal start and covariance values BT runMCMC: Optimization finished, setting startValues to 1.4901160971803e-08 - Setting covariance to 0.99999713415048
Running Metropolis-MCMC, chain iteration 100 of 1000 . Current logp: -3.915425 Please wait!
Running Metropolis-MCMC, chain iteration 200 of 1000 . Current logp: -3.952539 Please wait!
Running Metropolis-MCMC, chain iteration 300 of 1000 . Current logp: -4.330099 Please wait!
Running Metropolis-MCMC, chain iteration 400 of 1000 . Current logp: -4.801967 Please wait!
Running Metropolis-MCMC, chain iteration 500 of 1000 . Current logp: -4.04227 Please wait!
Running Metropolis-MCMC, chain iteration 600 of 1000 . Current logp: -4.129271 Please wait!
Running Metropolis-MCMC, chain iteration 700 of 1000 . Current logp: -4.062493 Please wait!
Running Metropolis-MCMC, chain iteration 800 of 1000 . Current logp: -4.430568 Please wait!
Running Metropolis-MCMC, chain iteration 900 of 1000 . Current logp: -3.943009 Please wait!
Running Metropolis-MCMC, chain iteration 1000 of 1000 . Current logp: -4.060668 Please wait! runMCMC terminated after 0.181secondsplot(out)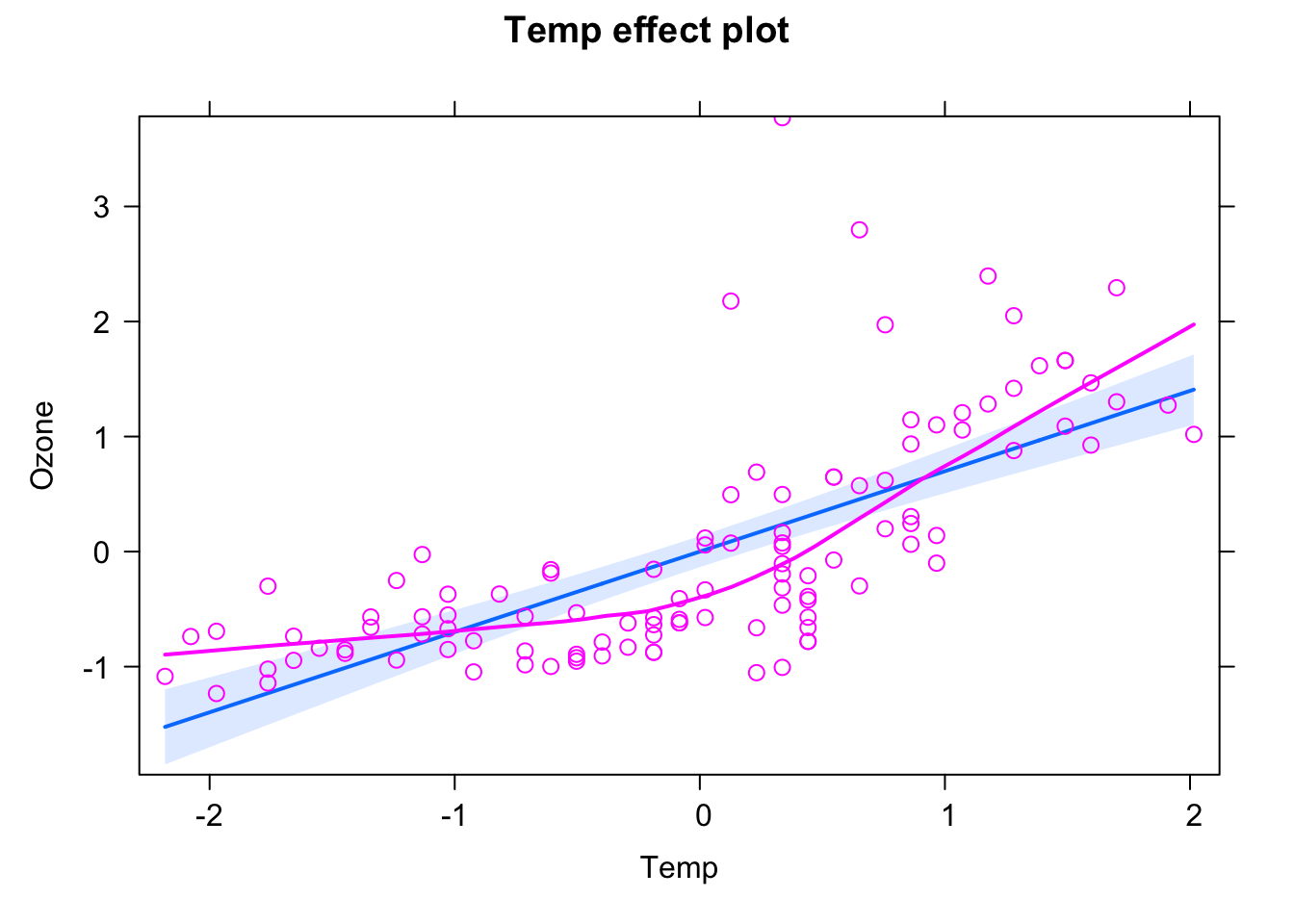
What we get as a result is the so-called trace plot to the left, which shows us how the sampler jumped around in parameter space over time, and the density plot to the right, which shows us results of sampling from the normal distribution.
For this simple case, this is not particularly impressive, and looks exactly like the plot that we coded above, using the seq approach. However, as discussed above, the first approach will break down if we have high-dimensional multivariate distributions, wheras MCMC sampling also works for high-dimensional problems.
Note
If you are interested in how an MCMC sampler works internally, you can look at Appendix (appendix-BayesianNumerics?).
3.2 Fitting a linear regression with different MCMCs
We will use the dataset airquality, just removing NAs and scaling all variables for convenience
airqualityCleaned = airquality[complete.cases(airquality),]
airqualityCleaned = data.frame(scale(airqualityCleaned))Our goal here is to fit the relationship between Ozone and Temperature with a linear regression
plot(Ozone ~ Temp, data = airqualityCleaned)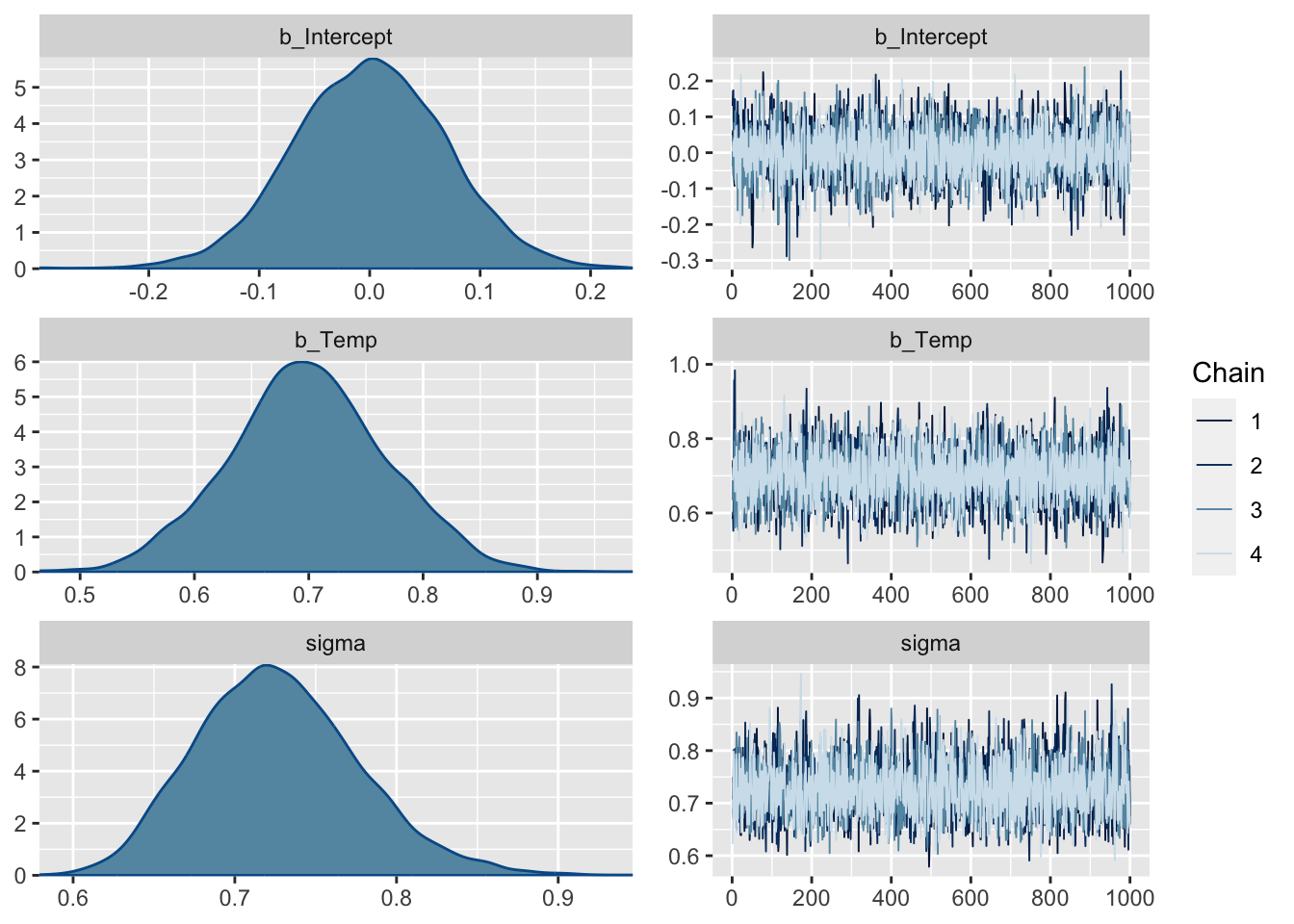
As a frequentist, you would do this via
fit <- lm(Ozone ~ Temp, data = airqualityCleaned)which would calculate the MLE an p-values for this model, and you could evaluate and summarize the results of this via
summary(fit)
library(effects)
plot(allEffects(fit, partial.residuals = T))
par(mfrow = c(2,2))
plot(fit) # residualsAs discussed above, as Bayesian, we have will estimate our models usually via MCMC sampling. Below, I show you three appraoches through which you can do this.
3.2.1 Bayesian analysis with brms
brms is a package that allows you to specify regression models in the formular syntax that is familiar to you from standard frequentist R function and packages such as lm, lme4, etc. The application is straightforward
In the background, brms will translate you command into a STAN model (see below), fit this model, and return the results!
summary(fit) Family: gaussian
Links: mu = identity; sigma = identity
Formula: Ozone ~ Temp
Data: airqualityCleaned (Number of observations: 111)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -0.00 0.07 -0.14 0.14 1.00 3725 2409
Temp 0.70 0.07 0.56 0.83 1.00 4106 2791
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.73 0.05 0.64 0.84 1.00 3308 2682
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).plot(fit, ask = FALSE)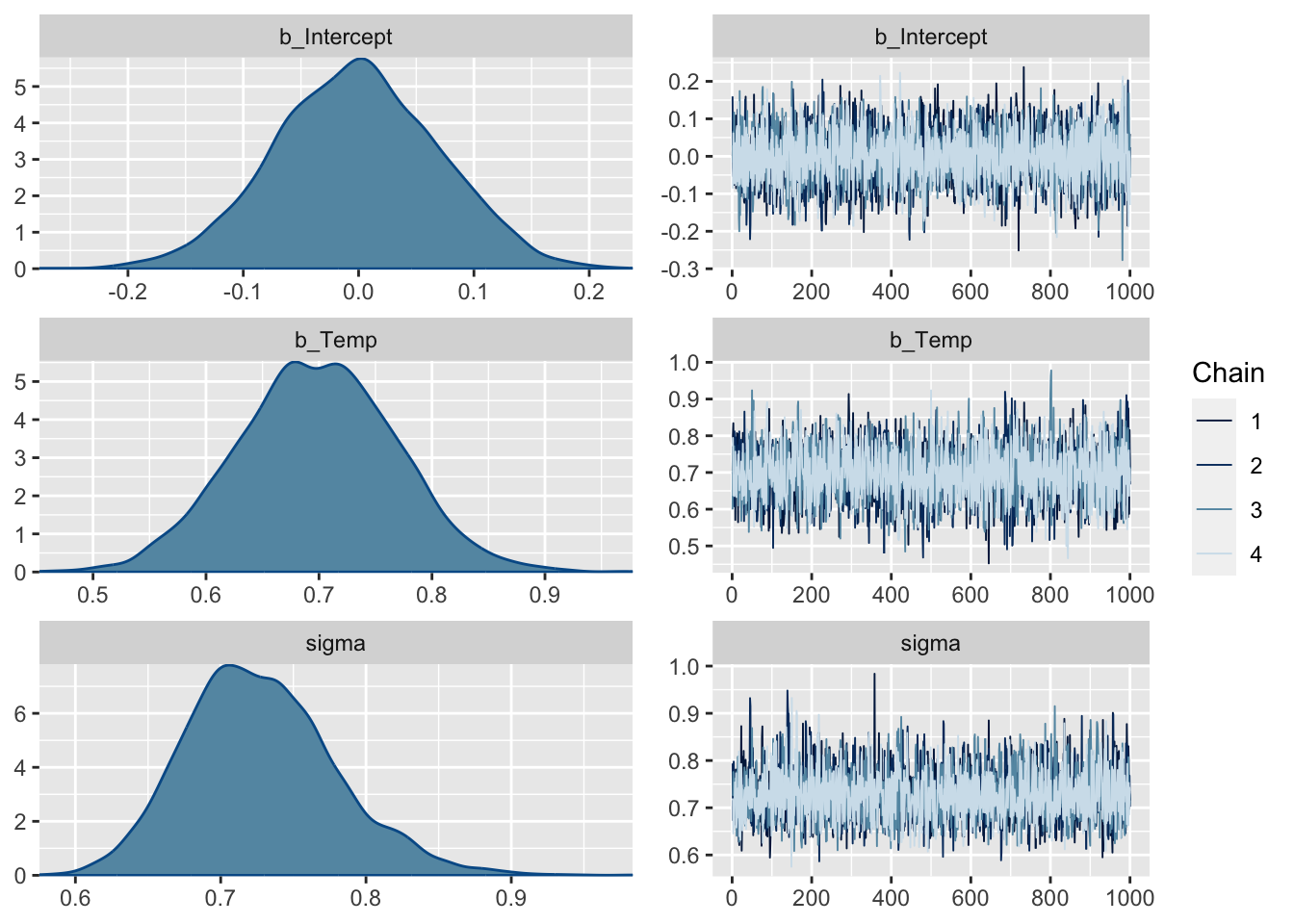
plot(conditional_effects(fit), ask = FALSE)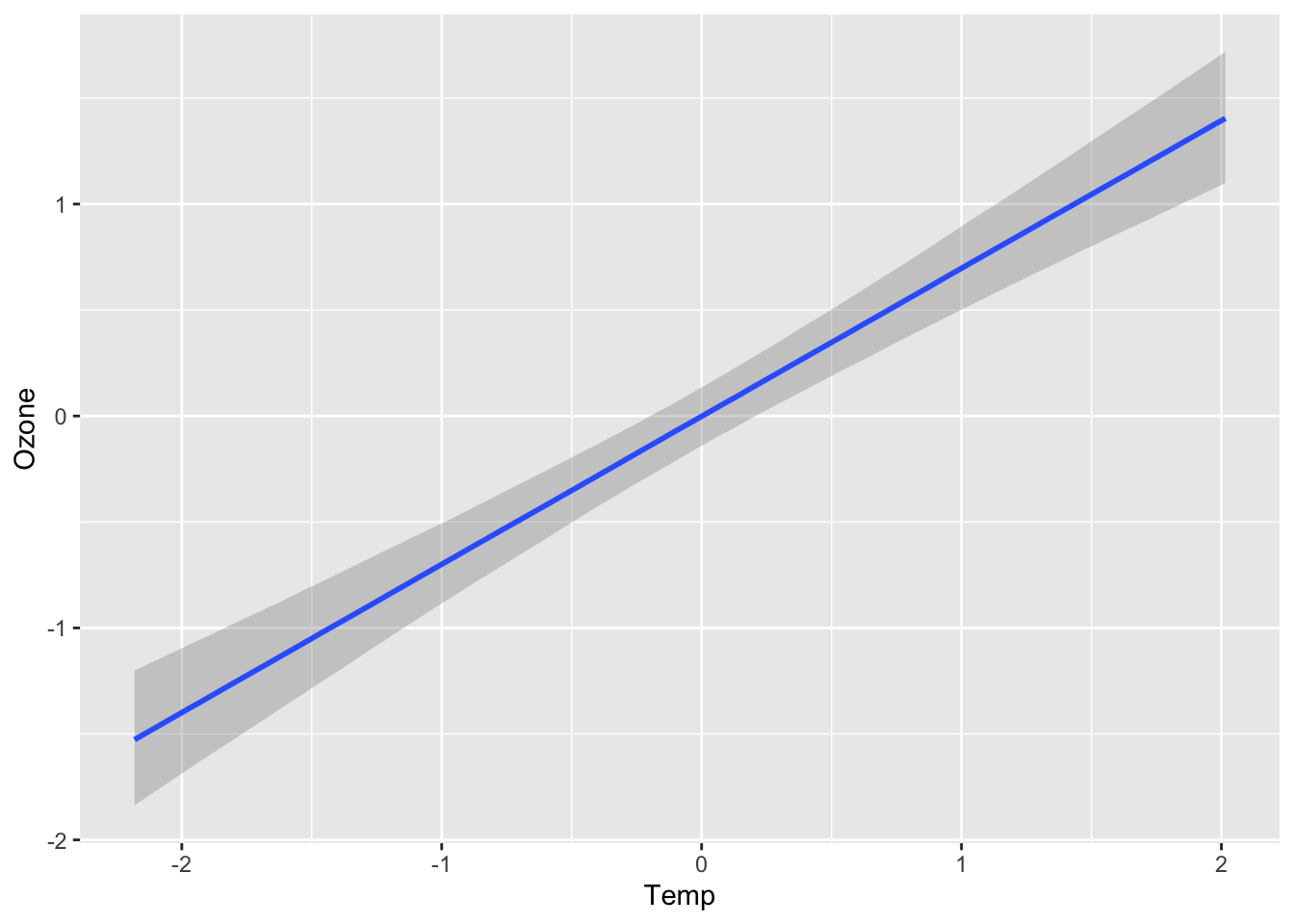
fit$model # model that is actually fit via // generated with brms 2.17.0
functions {
}
data {
int<lower=1> N; // total number of observations
vector[N] Y; // response variable
int<lower=1> K; // number of population-level effects
matrix[N, K] X; // population-level design matrix
int prior_only; // should the likelihood be ignored?
}
transformed data {
int Kc = K - 1;
matrix[N, Kc] Xc; // centered version of X without an intercept
vector[Kc] means_X; // column means of X before centering
for (i in 2:K) {
means_X[i - 1] = mean(X[, i]);
Xc[, i - 1] = X[, i] - means_X[i - 1];
}
}
parameters {
vector[Kc] b; // population-level effects
real Intercept; // temporary intercept for centered predictors
real<lower=0> sigma; // dispersion parameter
}
transformed parameters {
real lprior = 0; // prior contributions to the log posterior
lprior += student_t_lpdf(Intercept | 3, -0.3, 2.5);
lprior += student_t_lpdf(sigma | 3, 0, 2.5)
- 1 * student_t_lccdf(0 | 3, 0, 2.5);
}
model {
// likelihood including constants
if (!prior_only) {
target += normal_id_glm_lpdf(Y | Xc, Intercept, b, sigma);
}
// priors including constants
target += lprior;
}
generated quantities {
// actual population-level intercept
real b_Intercept = Intercept - dot_product(means_X, b);
}pp_check(fit) # residual checksUsing 10 posterior draws for ppc type 'dens_overlay' by default.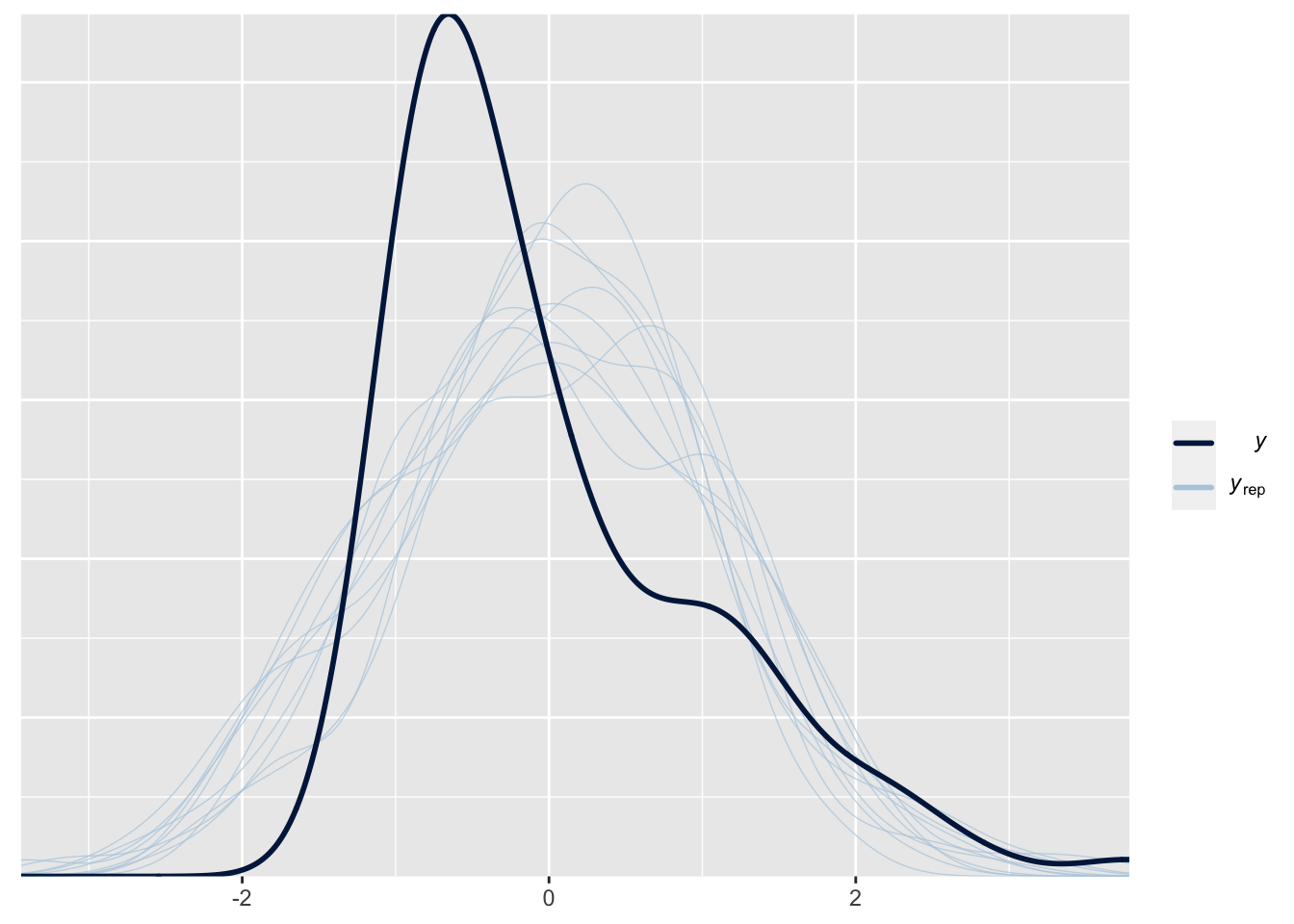
3.2.2 Bayesian analysis with JAGS
The general approach in JAGS is to
- Set up a list that contains all the necessary data
- Write the model as a string in the JAGS specific BUGS dialect
- Compile the model and run the MCMC for an adaptation (burn-in) phase
library(rjags)
Data = list(y = airqualityCleaned$Ozone, x = airqualityCleaned$Temp, nobs = nrow(airqualityCleaned))
modelCode = "
model{
# Likelihood
for(i in 1:nobs){
mu[i] <- a*x[i]+ b
y[i] ~ dnorm(mu[i],tau) # dnorm in jags parameterizes via precision = 1/sd^2
}
# Prior distributions
# For location parameters, normal choice is wide normal
a ~ dnorm(0,0.0001)
b ~ dnorm(0,0.0001)
# For scale parameters, normal choice is decaying
tau ~ dgamma(0.001, 0.001)
sigma <- 1/sqrt(tau) # this line is optional, just in case you want to observe sigma or set sigma (e.g. for inits)
}
"
# Specify a function to generate inital values for the parameters
# (optional, if not provided, will start with the mean of the prior )
inits.fn <- function() list(a = rnorm(1), b = rnorm(1), tau = 1/runif(1,1,100))
# sets up the model
jagsModel <- jags.model(file= textConnection(modelCode), data=Data, init = inits.fn, n.chains = 3)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 111
Unobserved stochastic nodes: 3
Total graph size: 310
Initializing model# MCMC sample from model
Samples <- coda.samples(jagsModel, variable.names = c("a","b","sigma"), n.iter = 5000)
# Plot the mcmc chain and the posterior sample
plot(Samples)
summary(Samples)
Iterations = 1:5000
Thinning interval = 1
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
a 0.698556 0.07055 0.0005760 0.0005714
b 0.001087 0.06872 0.0005611 0.0005611
sigma 0.724221 0.05136 0.0004194 0.0004313
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
a 0.5635 0.65237 0.6986556 0.74458 0.8345
b -0.1305 -0.04479 0.0006133 0.04712 0.1333
sigma 0.6350 0.68940 0.7210357 0.75549 0.83013.2.3 Bayesian analysis with STAN
Approach is identical to JAGS just that we have to define all variables in the section data
library(rstan)
stanmodelcode <- "
data {
int<lower=0> N;
vector[N] x;
vector[N] y;
}
parameters {
real alpha;
real beta;
real<lower=0> sigma;
}
model {
y ~ normal(alpha + beta * x, sigma);
}
"
dat = list(y = airqualityCleaned$Ozone, x = airqualityCleaned$Temp, N = nrow(airqualityCleaned))
fit <- stan(model_code = stanmodelcode, model_name = "example",
data = dat, iter = 2012, chains = 3, verbose = TRUE,
sample_file = file.path(tempdir(), 'norm.csv')) print(fit)Inference for Stan model: example.
3 chains, each with iter=2012; warmup=1006; thin=1;
post-warmup draws per chain=1006, total post-warmup draws=3018.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha 0.00 0.00 0.07 -0.14 -0.05 0.00 0.05 0.14 2759 1
beta 0.70 0.00 0.07 0.55 0.65 0.70 0.75 0.84 3024 1
sigma 0.73 0.00 0.05 0.63 0.69 0.73 0.76 0.84 3339 1
lp__ -19.79 0.04 1.33 -23.41 -20.31 -19.42 -18.84 -18.30 1346 1
Samples were drawn using NUTS(diag_e) at Tue Jul 2 11:25:51 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).plot(fit)ci_level: 0.8 (80% intervals)outer_level: 0.95 (95% intervals)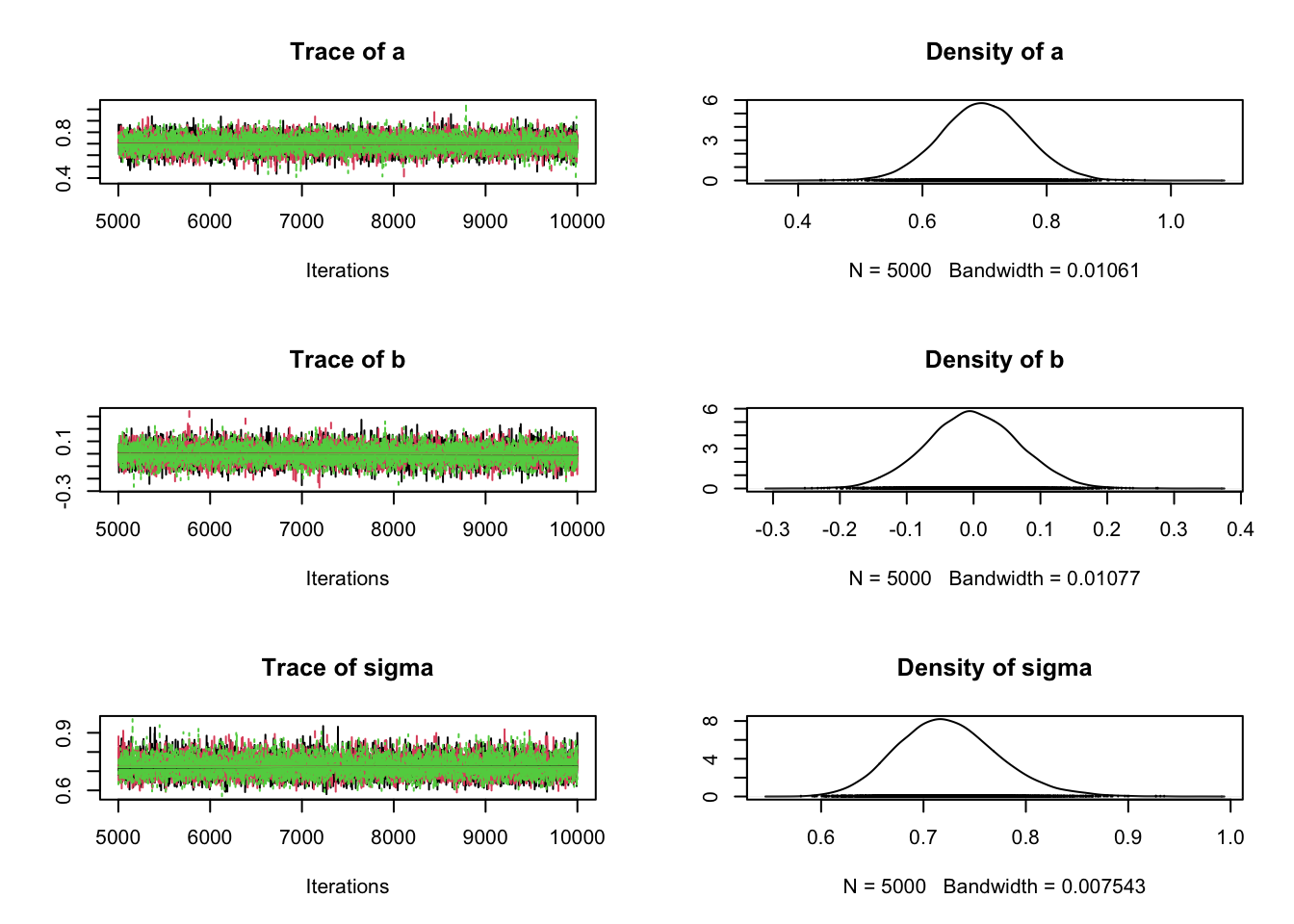
rstan::traceplot(fit)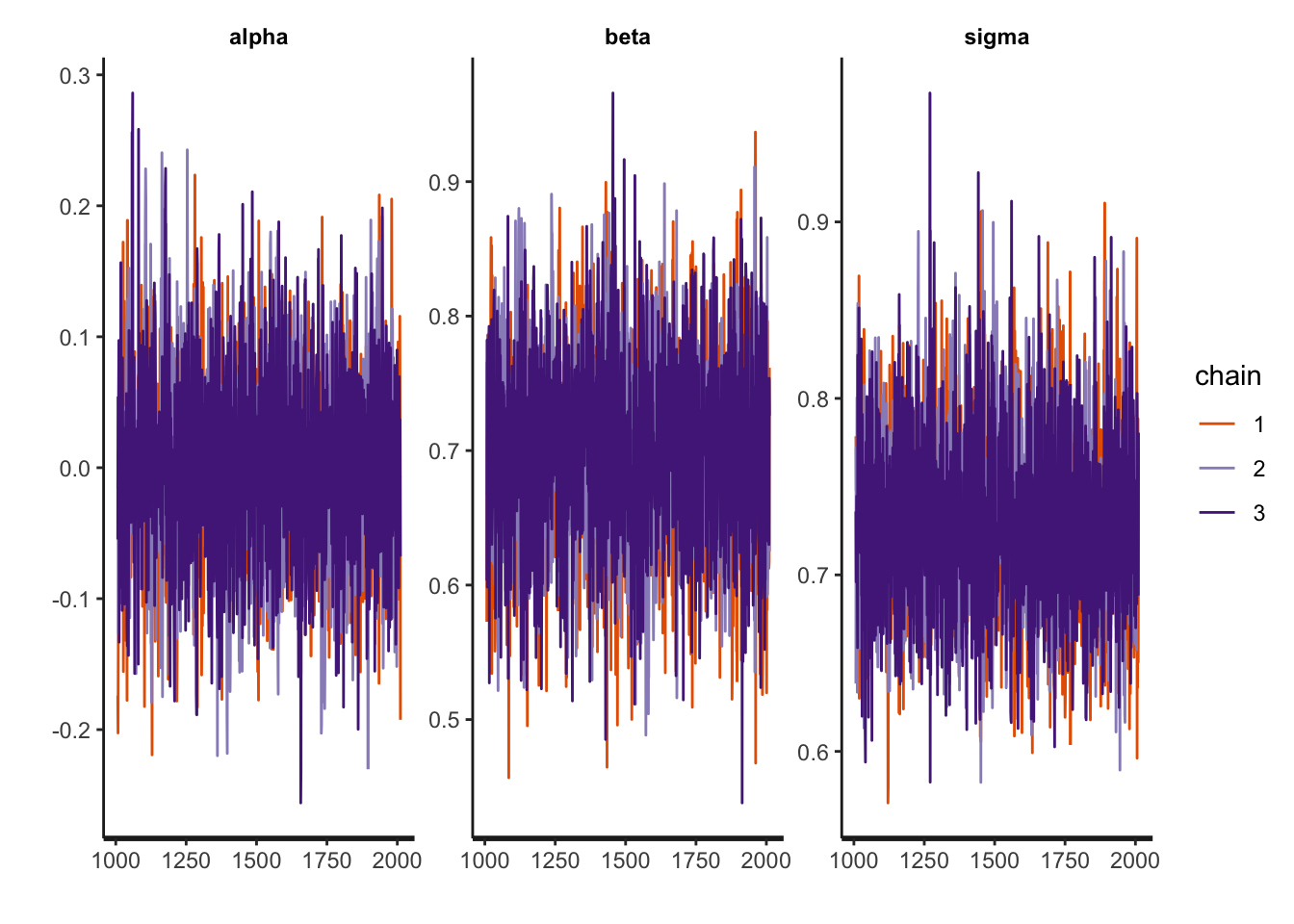
3.2.4 Bayesian analysis via BayesianTools
Here, we don’t use a model specification language, but just write out the likelihood as an standard R function. The same can be done for the prior. For simplicity, in this case I just used flat priors using the lower / upper arguments.
library(BayesianTools)
likelihood <- function(par){
a0 = par[1]
a1 = par[2]
sigma <- par[3]
logLikel = sum(dnorm(a0 + a1 * airqualityCleaned$Temp - airqualityCleaned$Ozone , sd = sigma, log = T))
return(logLikel)
}
setup <- createBayesianSetup(likelihood = likelihood, lower = c(-10,-10,0.01), upper = c(10,10,10), names = c("a0", "a1", "sigma"))
out <- runMCMC(setup)plot(out)
summary(out, start = 1000)# # # # # # # # # # # # # # # # # # # # # # # # #
## MCMC chain summary ##
# # # # # # # # # # # # # # # # # # # # # # # # #
# MCMC sampler: DEzs
# Nr. Chains: 3
# Iterations per chain: 2335
# Rejection rate: 0.777
# Effective sample size: 454
# Runtime: 0.929 sec.
# Parameters
psf MAP 2.5% median 97.5%
a0 1.006 0.003 -0.143 0.003 0.144
a1 1.012 0.702 0.560 0.692 0.822
sigma 1.005 0.709 0.635 0.722 0.828
## DIC: 270.119
## Convergence
Gelman Rubin multivariate psrf:
3.3 Checking and expecting the results
Running the sampler again
Samples <- coda.samples(jagsModel, variable.names = c("a","b","sigma"), n.iter = 5000)3.3.1 Convergence checks
Except for details in the syntax, the following is more or less the same for all samplers.
First thing should always be convergence checks. Visual look at the trace plots,
plot(Samples)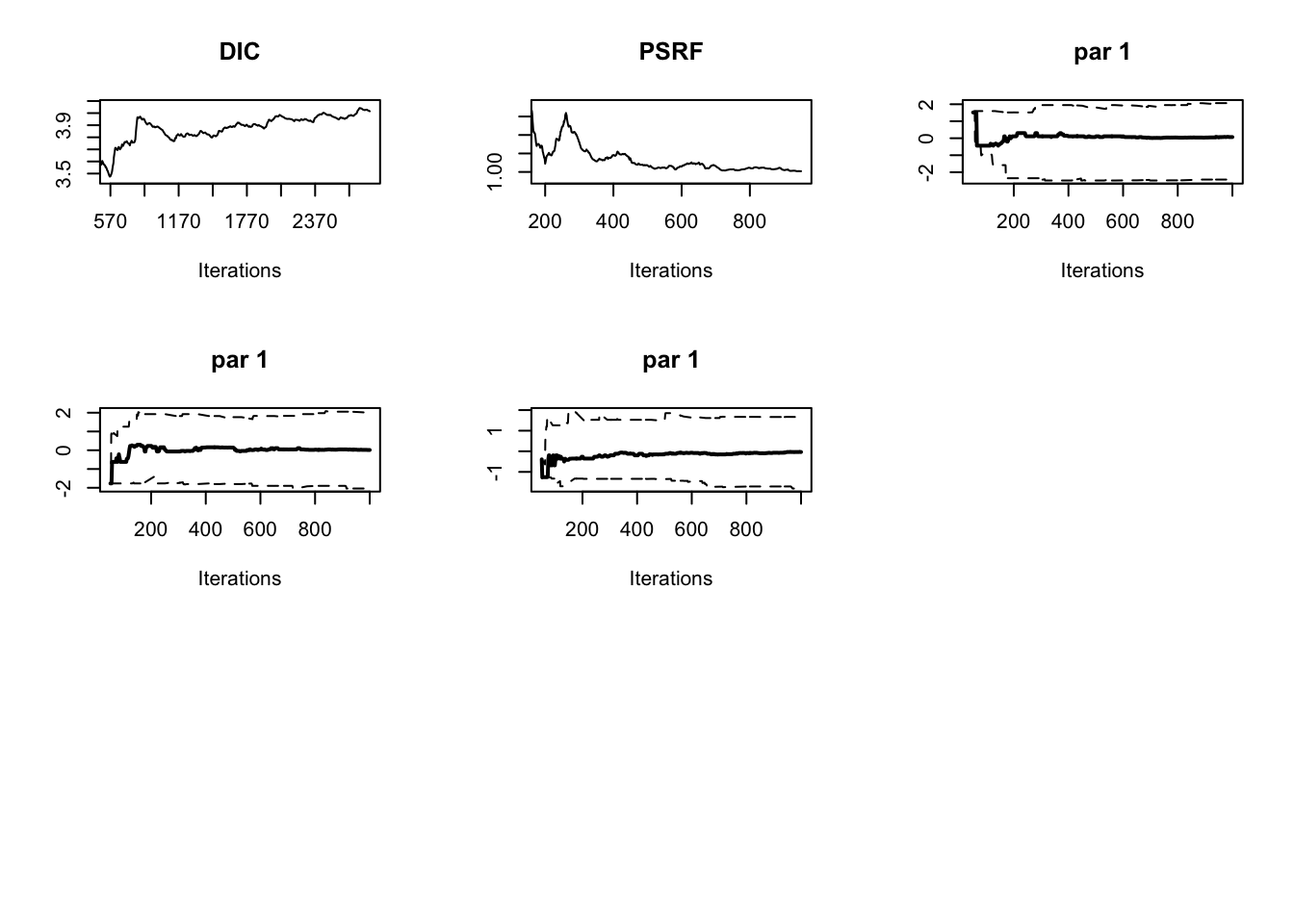
We want to look at
- Convergence to the right parameter area (seems immediate, else you will see a slow move of the parameters in the traceplot). You should set burn-in after you have converged to the right area
- Mixing: low autocorrelation in the chain after convergence to target area (seems excellent in this case)
Further convergence checks should be done AFTER removing burn-in
coda::acfplot(Samples)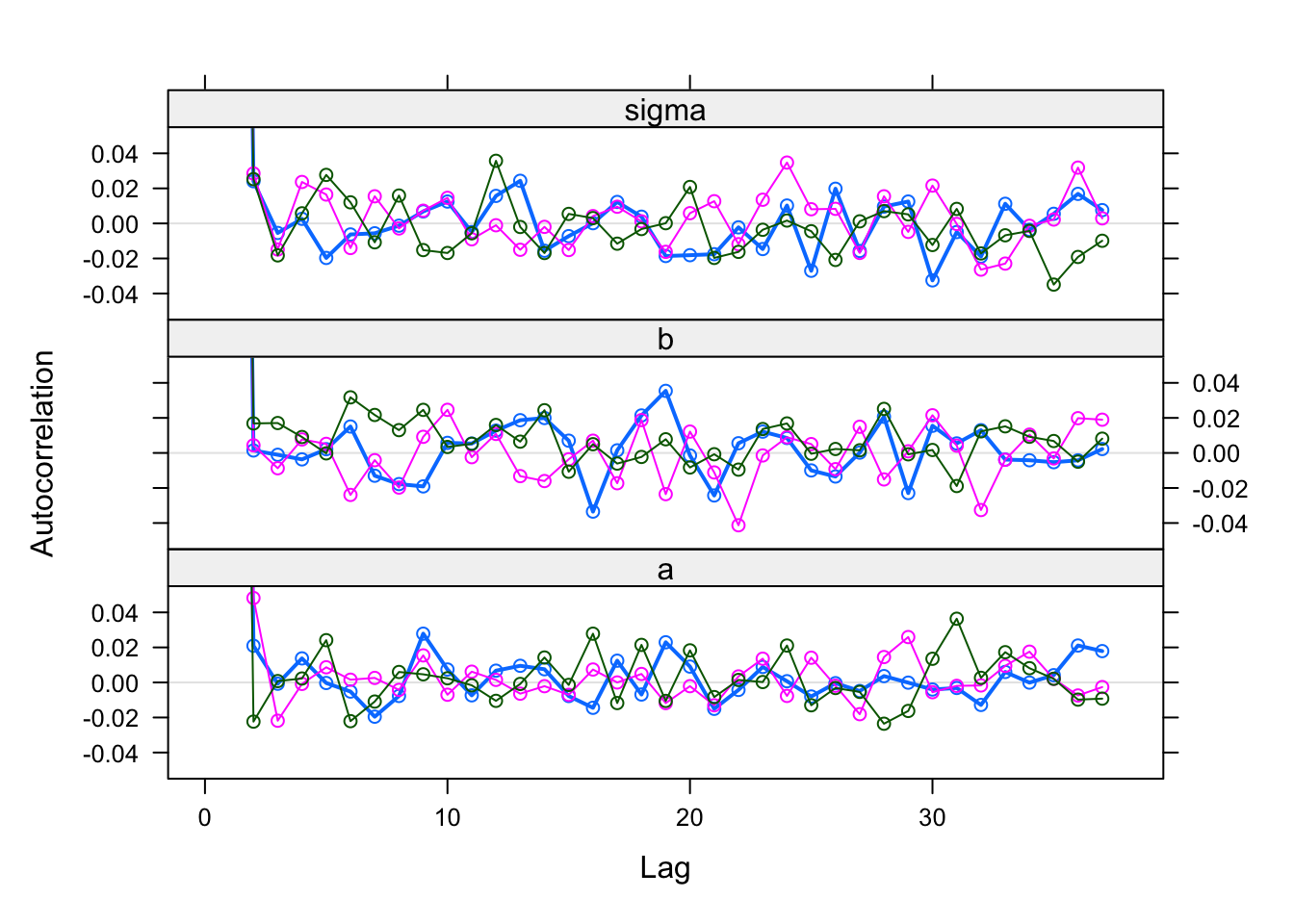
Formal convergence diagnostics via
coda::gelman.diag(Samples)Potential scale reduction factors:
Point est. Upper C.I.
a 1 1
b 1 1
sigma 1 1
Multivariate psrf
1coda::gelman.plot(Samples)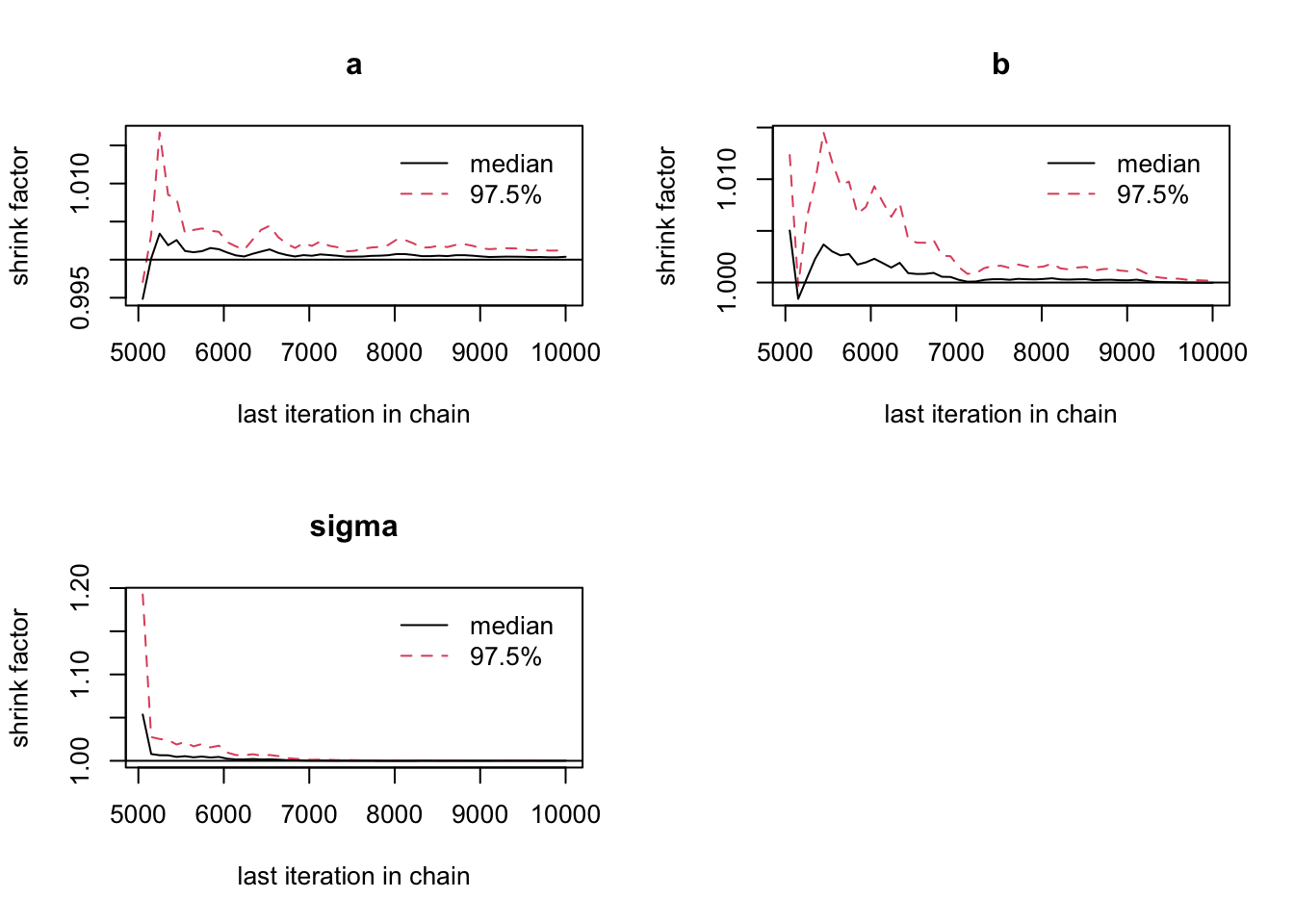
No fixed rule but typically people require univariate psrf < 1.05 or < 1.1 and multivariate psrf < 1.1 or 1.2
Caution
Note that the msrf rule was made for estimating the mean / median. If you want to estimate more unstable statistics, e.g. higher quantiles or other values such as the MAP or the DIC (see section on model selection), you may have to run the MCMC chain much longer to get stable outputs.
library(BayesianTools)
bayesianSetup <- createBayesianSetup(likelihood = testDensityNormal,
prior = createUniformPrior(lower = -10,
upper = 10))
out = runMCMC(bayesianSetup = bayesianSetup, settings = list(iterations = 3000))The plotDiagnostics function in package BT shows us how statistics develop over time
plotDiagnostic(out)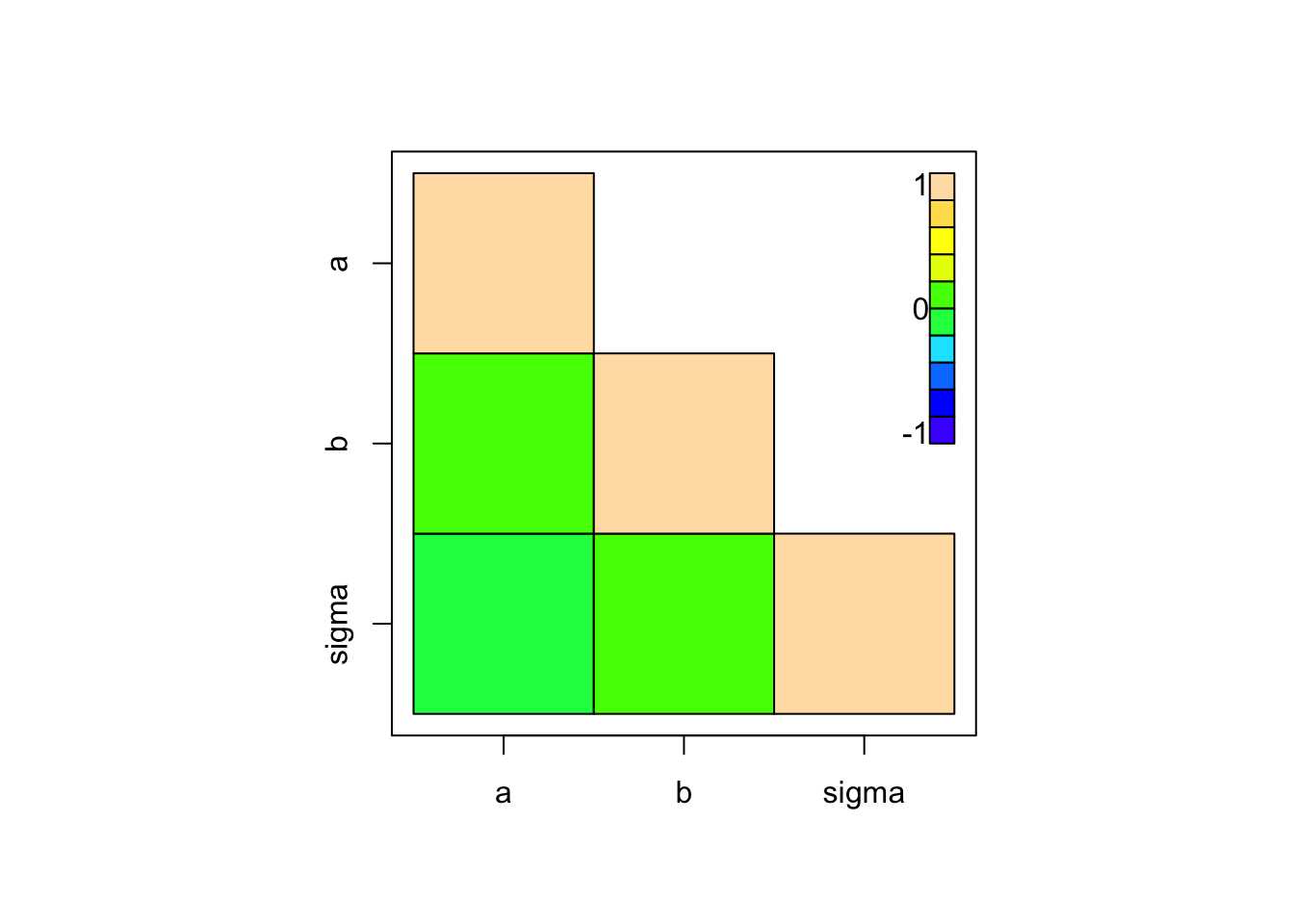
3.3.2 Summary Table
summary(Samples)
Iterations = 5001:10000
Thinning interval = 1
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
a 6.994e-01 0.06955 0.0005678 0.0005723
b -3.372e-05 0.06891 0.0005626 0.0005626
sigma 7.253e-01 0.05011 0.0004091 0.0004212
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
a 0.5635 0.65303 0.6989581 0.74574 0.8366
b -0.1337 -0.04608 -0.0004285 0.04616 0.1370
sigma 0.6355 0.68992 0.7219566 0.75761 0.8316Highest Posterior Density intervals
HPDinterval(Samples)[[1]]
lower upper
a 0.5684561 0.8435704
b -0.1378257 0.1334005
sigma 0.6342108 0.8268713
attr(,"Probability")
[1] 0.95
[[2]]
lower upper
a 0.5636098 0.8309431
b -0.1365890 0.1344200
sigma 0.6303167 0.8242163
attr(,"Probability")
[1] 0.95
[[3]]
lower upper
a 0.5657504 0.8386521
b -0.1290830 0.1373207
sigma 0.6260861 0.8223699
attr(,"Probability")
[1] 0.953.3.3 Plots
Marginal plots show the parameter distribution (these were also created in the standard coda traceplots)
BayesianTools::marginalPlot(Samples)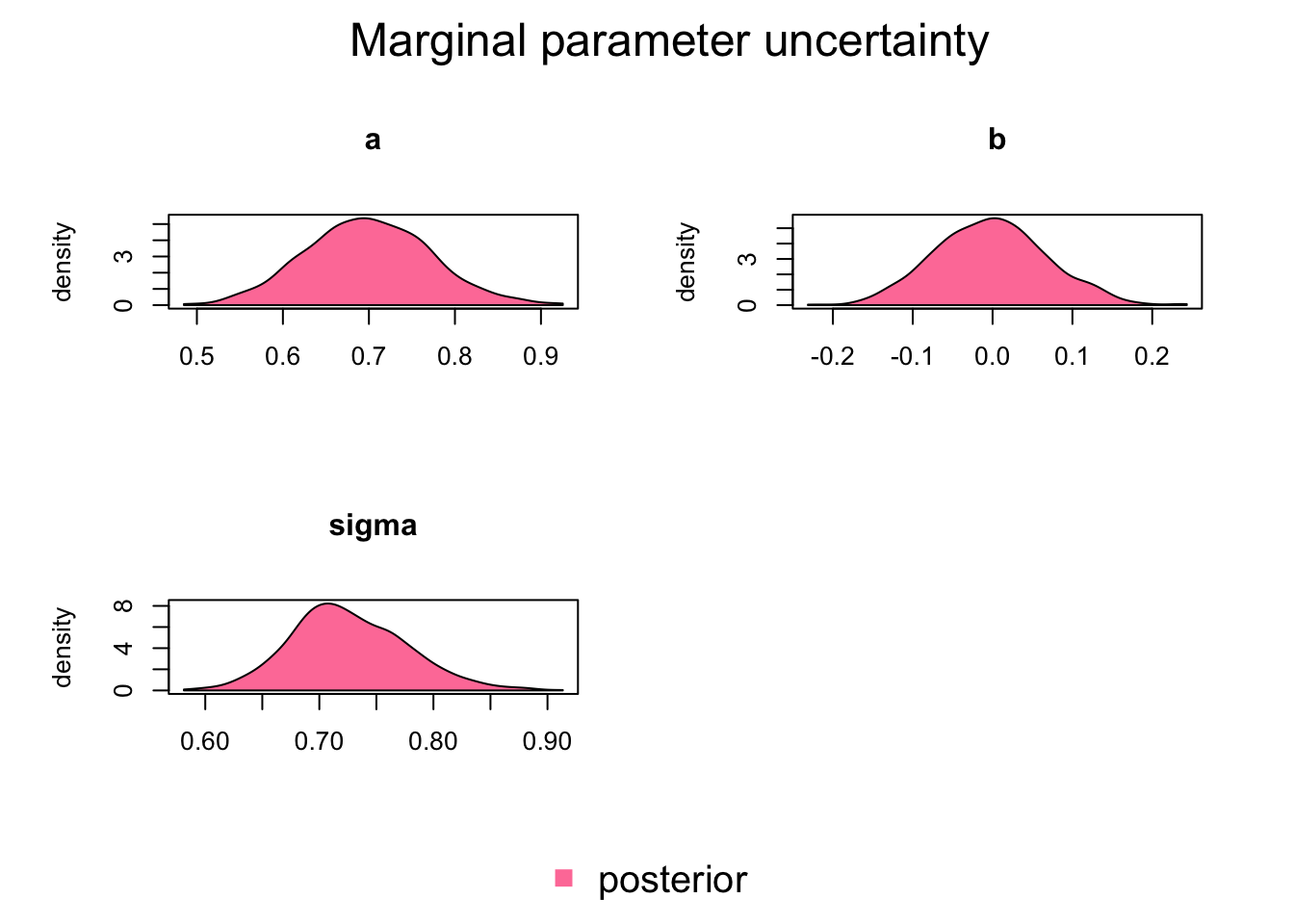
Pair correlation plots show 2nd order correlations
# coda
coda::crosscorr.plot(Samples)
#BayesianTools
correlationPlot(Samples)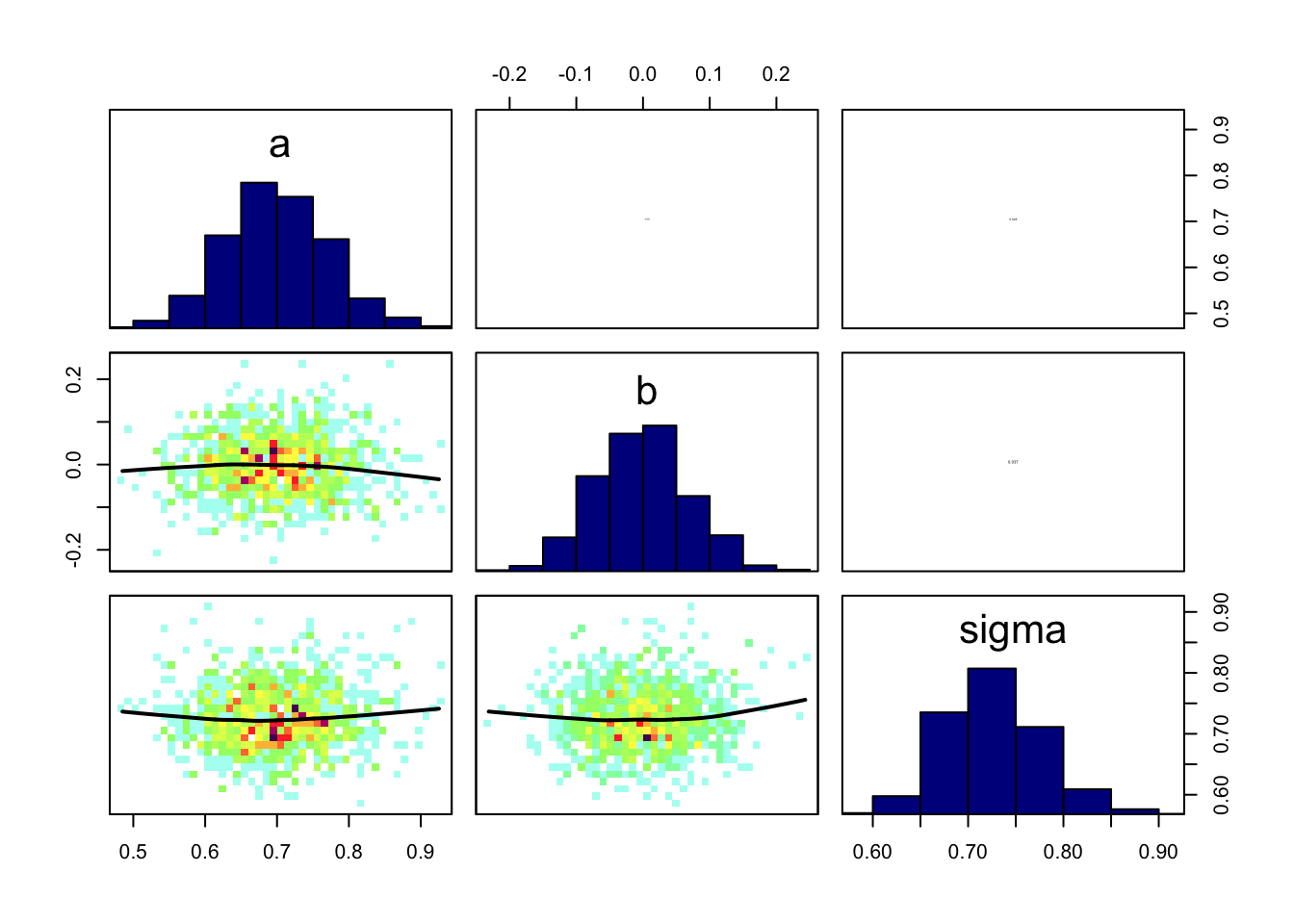
3.3.4 Posterior predictive distribution
dat = as.data.frame(Data)[,1:2]
dat = dat[order(dat$x),]
# raw data
plot(dat[,2], dat[,1])
# extract 1000 parameters from posterior from package BayesianTools
x = getSample(Samples, start = 300)
pred = x[,2] + dat[,2] %o% x[,1]
lines(dat[,2], apply(pred, 1, median))
lines(dat[,2], apply(pred, 1, quantile, probs = 0.2),
lty = 2, col = "red")
lines(dat[,2], apply(pred, 1, quantile, probs = 0.8),
lty = 2, col = "red")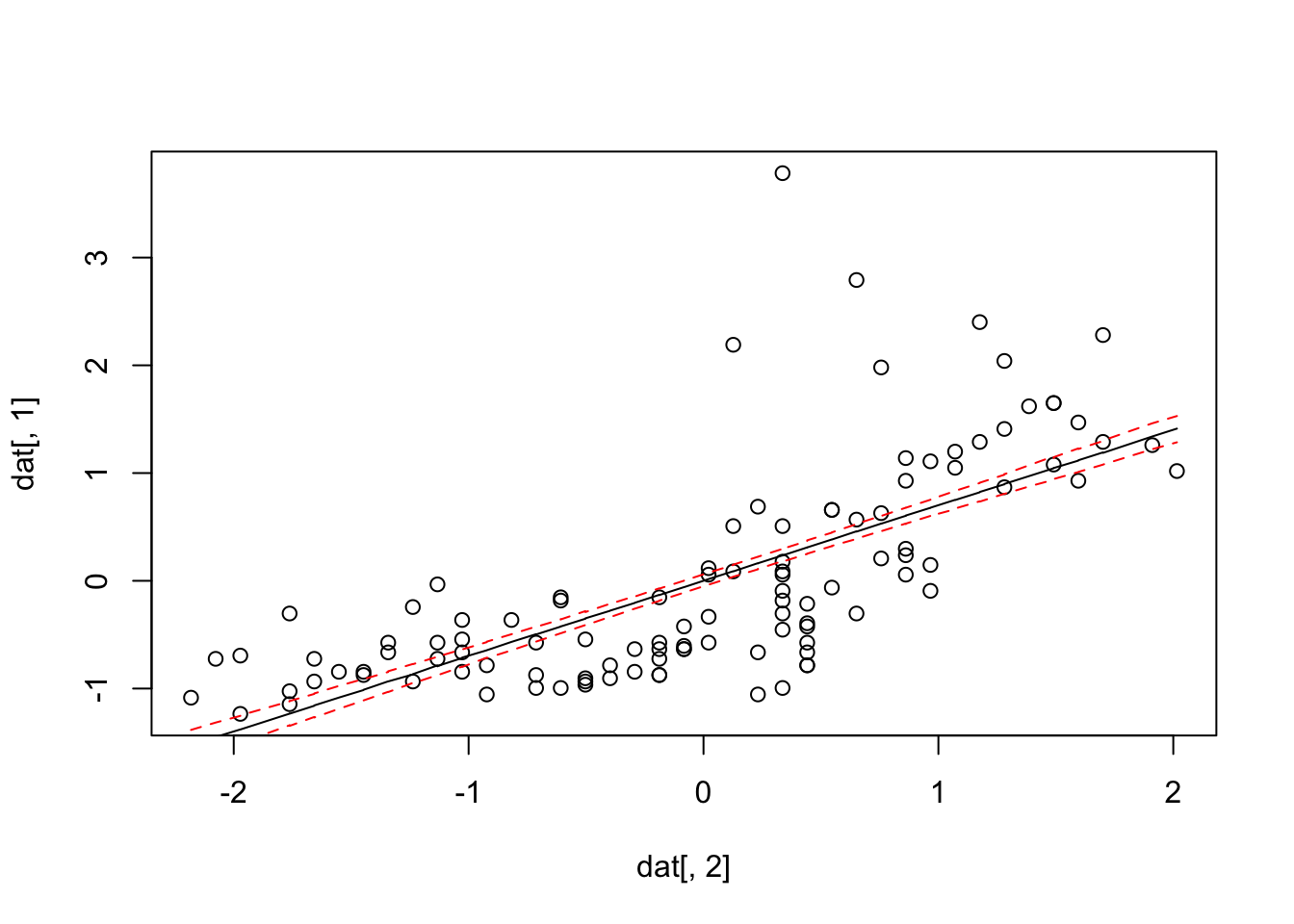
# alternative: plot all 1000 predictions in transparent color
plot(dat[,2], dat[,1])
for(i in 1:nrow(x)) lines(dat[,2], pred[,i], col = "#0000EE03")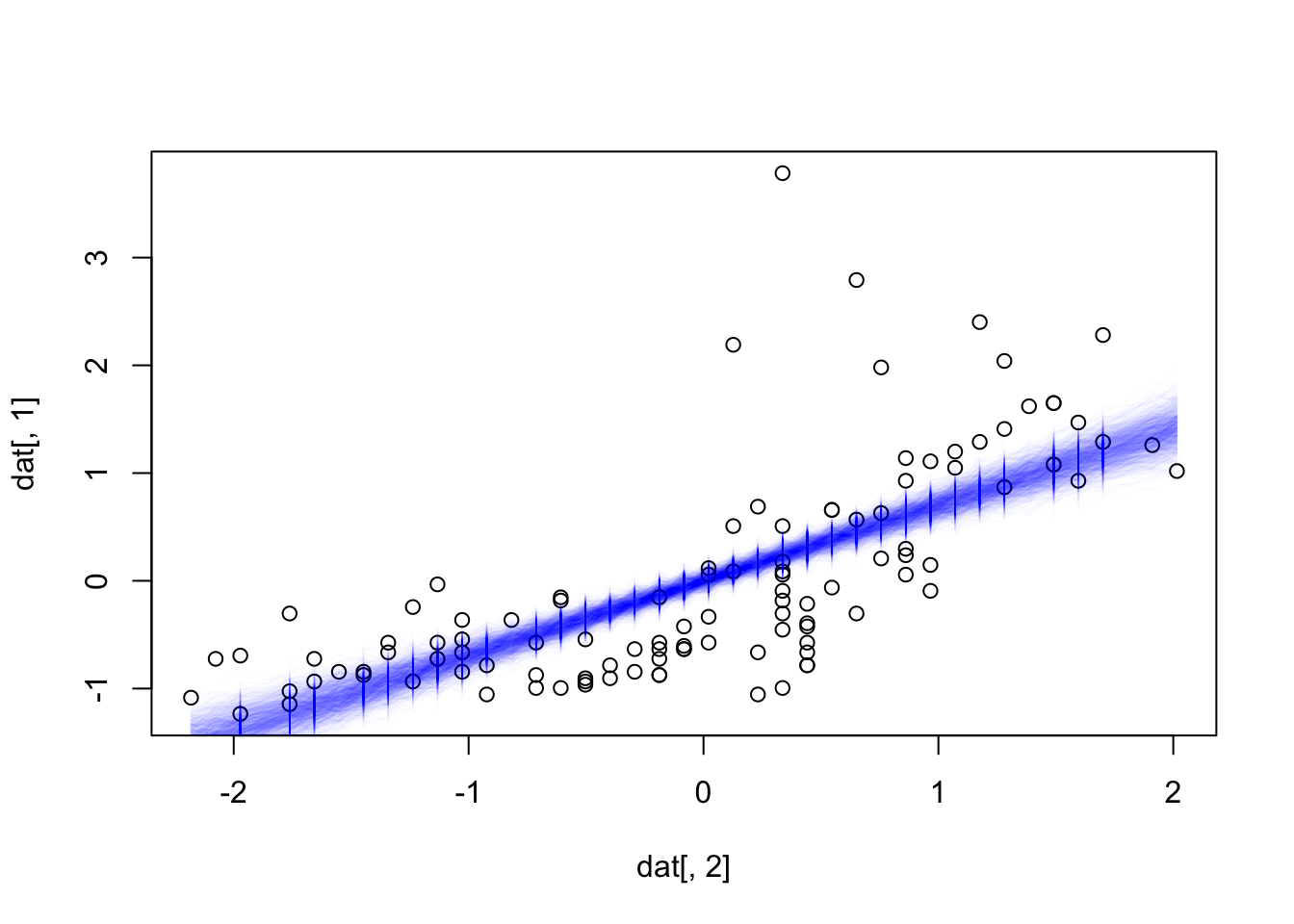
# important point - so far, we have plotted
# in frequentist, this is know as the confidence vs. the prediction distribution
# in the second case, we add th
pred = x[,2] + dat[,2] %o% x[,1]
for(i in 1:nrow(x)) {
pred[,i] = pred[,i] + rnorm(length(pred[,i]), 0, sd = x[i,3])
}
plot(dat[,2], dat[,1])
lines(dat[,2], apply(pred, 1, median))
lines(dat[,2], apply(pred, 1, quantile, probs = 0.2), lty = 2, col = "red")
lines(dat[,2], apply(pred, 1, quantile, probs = 0.8), lty = 2, col = "red")
#alternative plotting
polygon(x = c(dat[,2], rev(dat[,2])),
y = c(apply(pred, 1, quantile, probs = 0.2),
rev(apply(pred, 1, quantile, probs = 0.8))),
col = "#EE000020")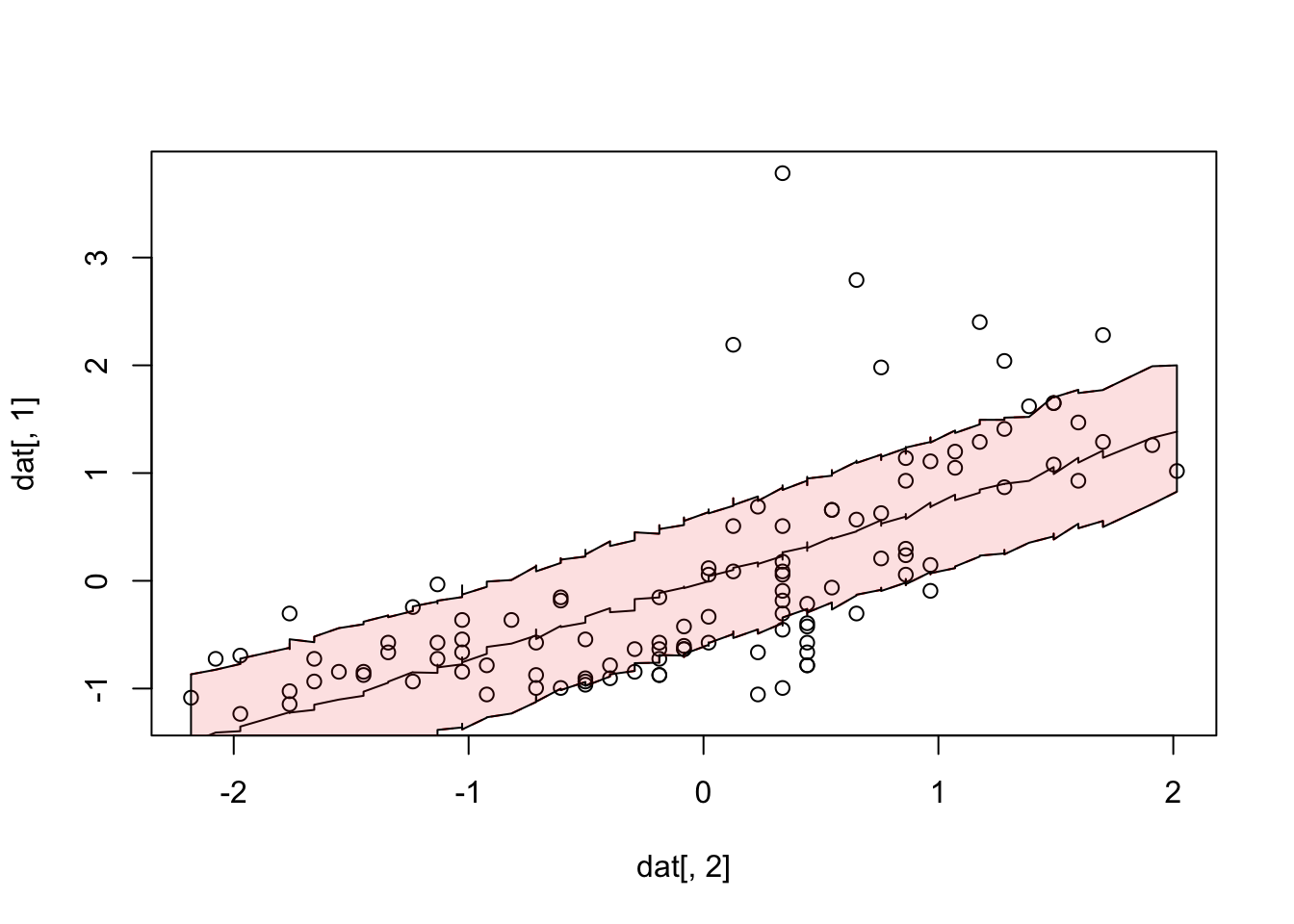
3.4 Playing around with the pipeline
3.4.1 Prior choice
Priors are not scale-free. What that means: dnorm(0,0.0001) might not be an uninformative prior, if the data scale is extremely small so that you might expect huge effect sizes - scaling all variables makes sure we have a good intuition of what “uninformative means”.
Task: play with the following minimal script for a linear regression to understand how scaling parameter affects priors and thus posterior shapes. In particular, change
- Multiply Ozone by 1000000 -> will push sd estimates high
- Multiply Temp by 0.0000001 -> will push parameter estimates high
Then compare Bayesian parameter estimates and their uncertainty to Bayesian estimates. How would you have to change the priors to fix this problem and keep them uninformative?
Task: 2 implement mildly informative priors as well as strong shrinkage priors in the regression. Question to discuss: should you put the shrinkage also in the intercept? Why should you center center variables if you include a shrinkage prior on the intercept?
library(rjags)
dat = airquality[complete.cases(airquality),]
# scaling happens here - change
dat$Ozone = as.vector(scale(dat$Ozone))
dat$Temp = as.vector(scale(dat$Temp))
Data = list(y = dat$Ozone,
x = dat$Temp,
i.max = nrow(dat))
# Model
modelCode = "
model{
# Likelihood
for(i in 1:i.max){
mu[i] <- Temp*x[i]+ intercept
y[i] ~ dnorm(mu[i],tau)
}
# Prior distributions
# For location parameters, typical choice is wide normal
intercept ~ dnorm(0,0.0001)
Temp ~ dnorm(0,0.0001)
# For scale parameters, typical choice is decaying
tau ~ dgamma(0.001, 0.001)
sigma <- 1/sqrt(tau) # this line is optional, just in case you want to observe sigma or set sigma (e.g. for inits)
}
"
# Specify a function to generate inital values for the parameters (optional, if not provided, will start with the mean of the prior )
inits.fn <- function() list(a = rnorm(1), b = rnorm(1),
tau = 1/runif(1,1,100))
# Compile the model and run the MCMC for an adaptation (burn-in) phase
jagsModel <- jags.model(file= textConnection(modelCode), data=Data, init = inits.fn, n.chains = 3)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 111
Unobserved stochastic nodes: 3
Total graph size: 310Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "a" in chain 1Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "b" in chain 1Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "a" in chain 2Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "b" in chain 2Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "a" in chain 3Warning in jags.model(file = textConnection(modelCode), data = Data, init =
inits.fn, : Unused initial value for "b" in chain 3Initializing model# Run a bit to have a burn-in
update(jagsModel, n.iter = 1000)
# Continue the MCMC runs with sampling
Samples <- coda.samples(jagsModel, variable.names = c("intercept","Temp","sigma"), n.iter = 5000)
# Bayesian results
summary(Samples)
Iterations = 1001:6000
Thinning interval = 1
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
Temp 0.6984643 0.06891 0.0005627 0.0005679
intercept -0.0002989 0.06872 0.0005611 0.0005611
sigma 0.7243984 0.04956 0.0004046 0.0004088
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
Temp 0.5628 0.65241 0.6987757 0.74428 0.8339
intercept -0.1363 -0.04603 0.0003719 0.04624 0.1342
sigma 0.6358 0.69009 0.7212351 0.75629 0.8286# MCMC results
fit <- lm(Ozone ~ Temp, data = dat)
summary(fit)
Call:
lm(formula = Ozone ~ Temp, data = dat)
Residuals:
Min 1Q Median 3Q Max
-1.2298 -0.5247 -0.0263 0.3138 3.5485
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.232e-17 6.823e-02 0.00 1
Temp 6.985e-01 6.854e-02 10.19 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.7188 on 109 degrees of freedom
Multiple R-squared: 0.488, Adjusted R-squared: 0.4833
F-statistic: 103.9 on 1 and 109 DF, p-value: < 2.2e-163.4.2 Missing data
In the analysis above, we removed missing data. What happens if you are leaving the missing data in in a Jags model? Try it out and discuss what happens