SMC sampler
Sequential Monte Carlo Sampler
smcSampler(bayesianSetup, initialParticles = 1000, iterations = 10, resampling = T, resamplingSteps = 2, proposal = NULL, adaptive = T, proposalScale = 0.5, likelihoodWeights = NULL)
Arguments
| bayesianSetup | either an object of class bayesianSetup created by |
|---|---|
| initialParticles | initial particles - either a draw from the prior, provided as a matrix with the single parameters as columns and each row being one particle (parameter vector), or a numeric value with the number of desired particles. In this case, the sampling option must be provided in the prior of the BayesianSetup. |
| iterations | number of iterations |
| resampling | if new particles should be created at each iteration |
| resamplingSteps | how many resampling (MCMC) steps between the iterations |
| proposal | optional proposal class |
| adaptive | should the covariance of the proposal be adapted during sampling |
| proposalScale | scaling factor for the proposal generation. Can be adapted if there is too much / too little rejection |
| likelihoodWeights | NULL, numeric vector, or function. The sum of all weights must be one, and the length of the vector must be equal to iterations. The value of the nth element determines the weight for the likelihood in the nth iteration. |
Details
The sampler can be used for rejection sampling as well as for sequential Monte Carlo. For the former case set the iterations to one.
Note
The SMC currently assumes that the initial particle is sampled from the prior. If a better initial estimate of the posterior distribution is available, this the sampler should be modified to include this. Currently, however, this is not included in the code, so the appropriate adjustments have to be done by hand.
Examples
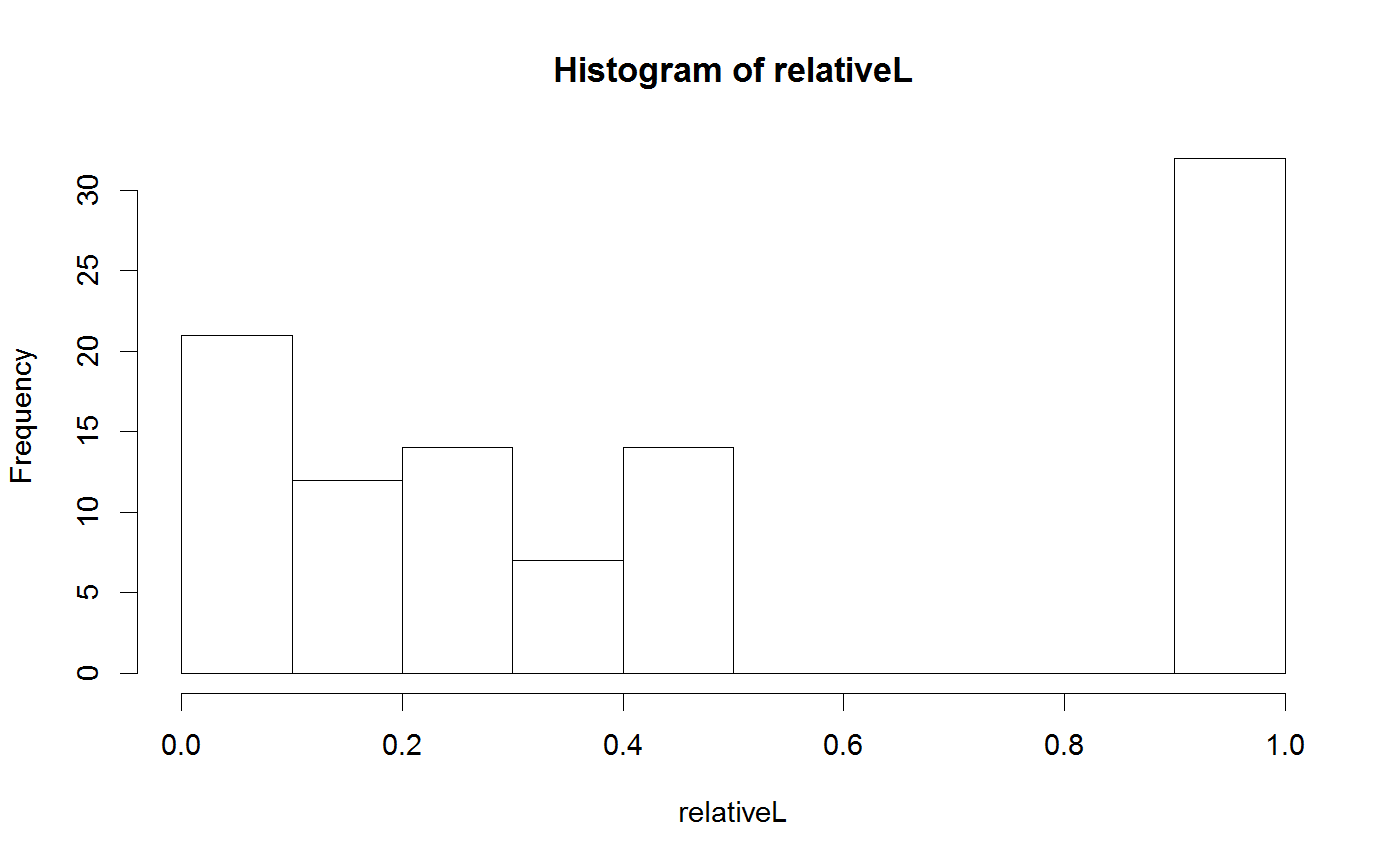
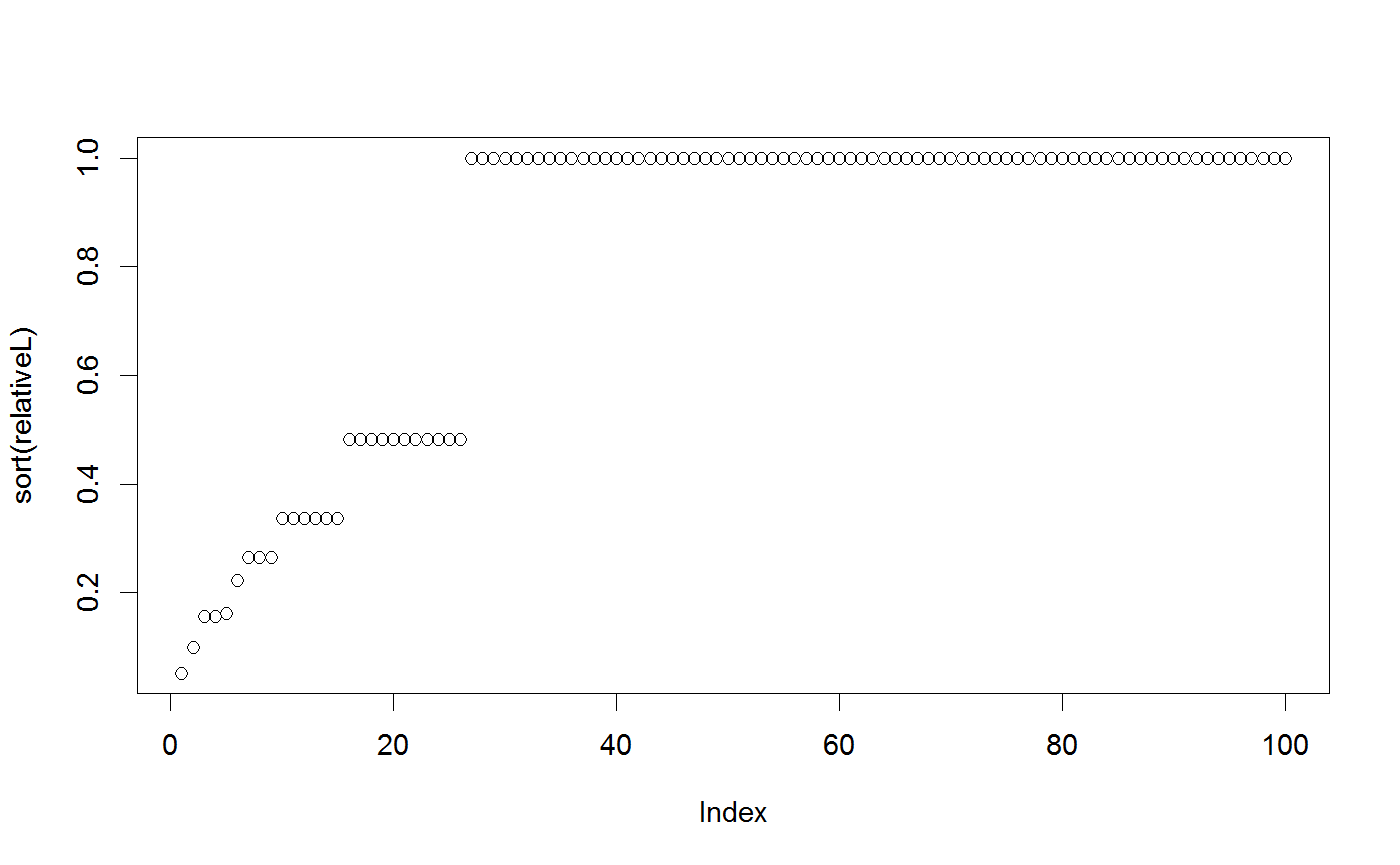
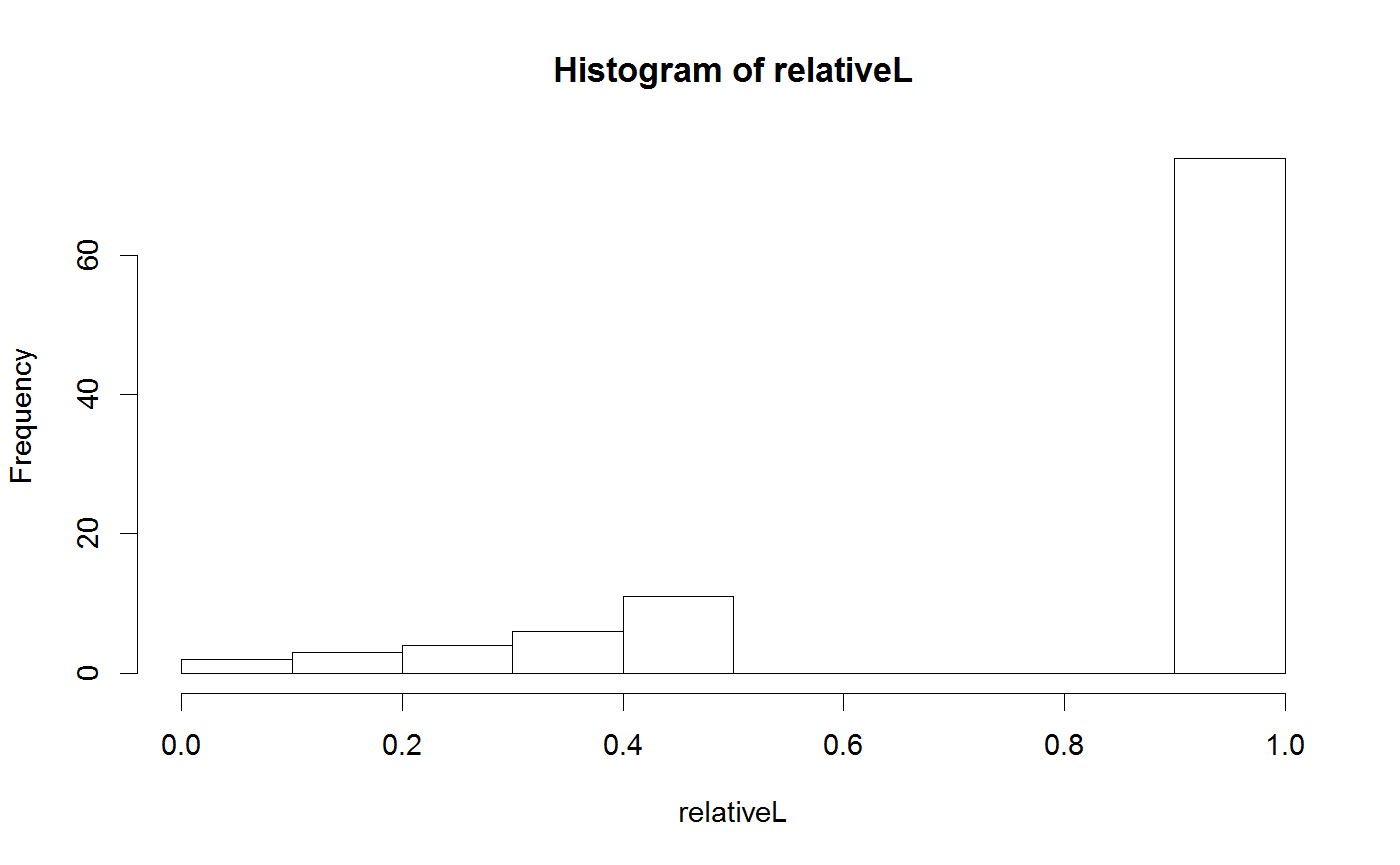
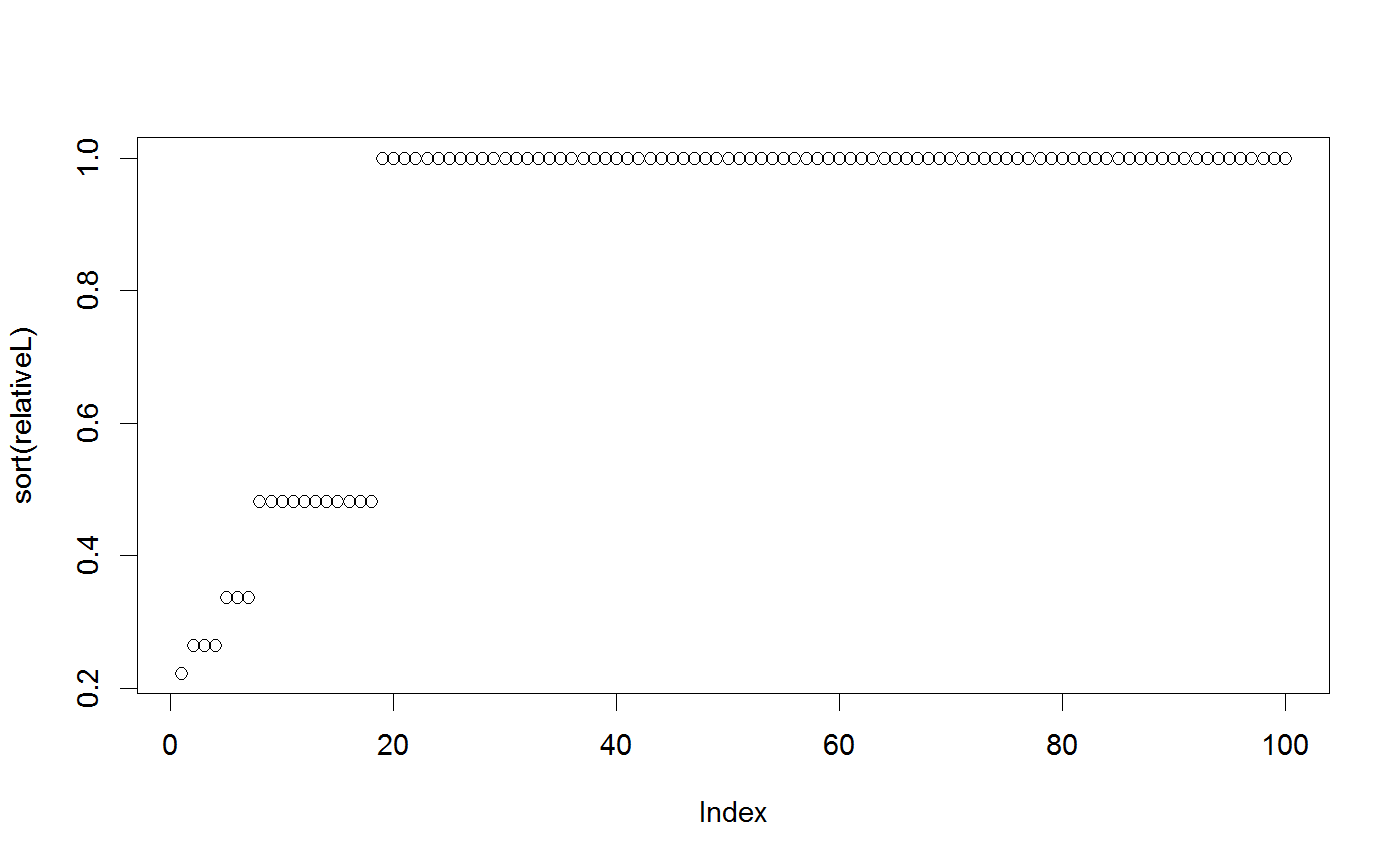
## Example for the use of SMC # First we need a bayesianSetup - SMC makes most sense if we can for demonstration, # we'll write a function that puts out the number of model calls MultiNomialNoCor <- generateTestDensityMultiNormal(sigma = "no correlation") parallelLL <- function(parMatrix){ print(paste("Calling likelihood with", nrow(parMatrix), "parameter combinations")) out = apply(parMatrix, 1, MultiNomialNoCor) return(out) } bayesianSetup <- createBayesianSetup(likelihood = parallelLL, lower = rep(-10, 3), upper = rep(10, 3), parallel = "external") # Defining settings for the sampler # First we use the sampler for rejection sampling settings <- list(initialParticles = 1000, iterations = 1, resampling = FALSE) # Running the sampler out1 <- runMCMC(bayesianSetup = bayesianSetup, sampler = "SMC", settings = settings)#> [1] 1 #> [1] "Calling likelihood with 1000 parameter combinations" #> [1] 2.984645#> [1] 26#>#plot(out1) # Now for sequential Monte Carlo settings <- list(initialParticles = 100, iterations = 5, resamplingSteps = 1) out2 <- runMCMC(bayesianSetup = bayesianSetup, sampler = "SMC", settings = settings)#> [1] 0.2 0.2 0.2 0.2 0.2 #> [1] "Calling likelihood with 100 parameter combinations" #> [1] 3.31721#> [1] 17 #> [1] "Calling likelihood with 2 parameter combinations" #> [1] "Calling likelihood with 100 parameter combinations" #> [1] 47.89169#> [1] 49 #> [1] "Calling likelihood with 2 parameter combinations" #> [1] "Calling likelihood with 100 parameter combinations" #> [1] 82.96134#> [1] 66 #> [1] "Calling likelihood with 3 parameter combinations" #> [1] "Calling likelihood with 100 parameter combinations" #> [1] 89.32615#> [1] 63 #> [1] "Calling likelihood with 100 parameter combinations" #> [1] 95.49201#> [1] 63 #> [1] "Calling likelihood with parameter combinations" #> Parameter values -7.49454366195938 -6.57156059686812 -7.17224688752869#> Warning: Problem encountered in the calculation of the likelihood with parameter -7.49454366195938-6.57156059686812-7.17224688752869 #> Error message wasError in apply(parMatrix, 1, MultiNomialNoCor): dim(X) must have a positive length #> #> set result of the parameter evaluation to -Inf ParaeterValues#>#plot(out2)