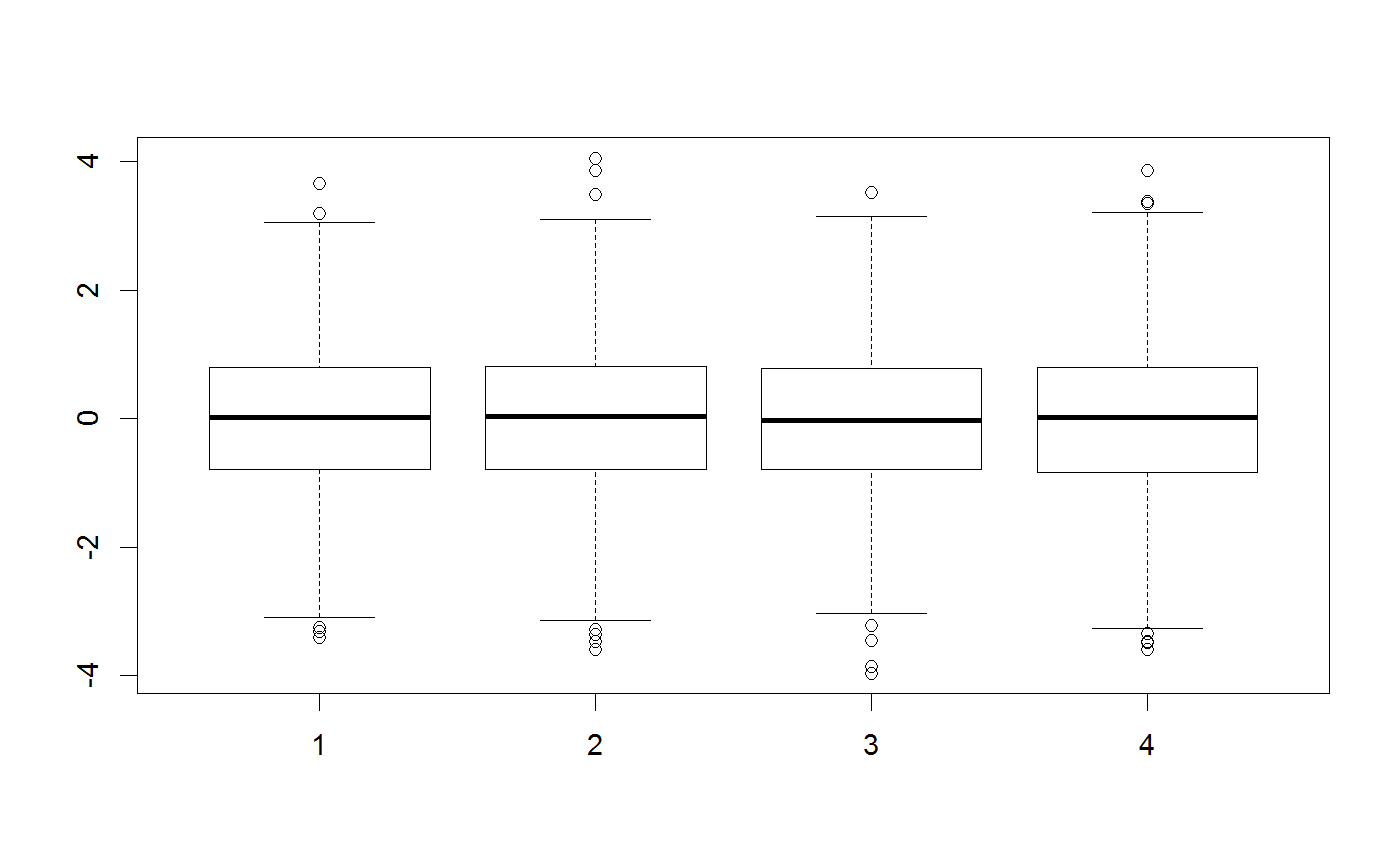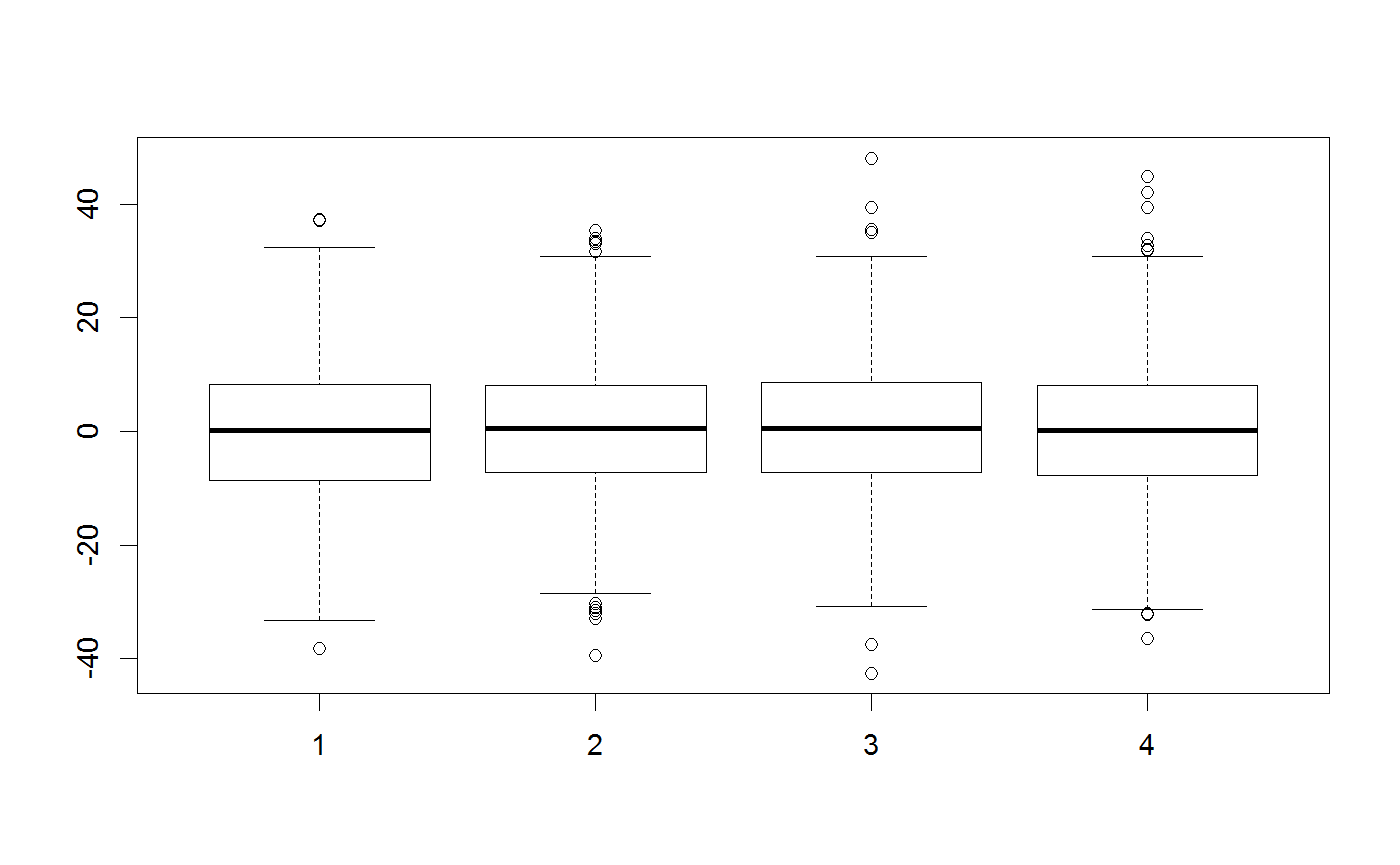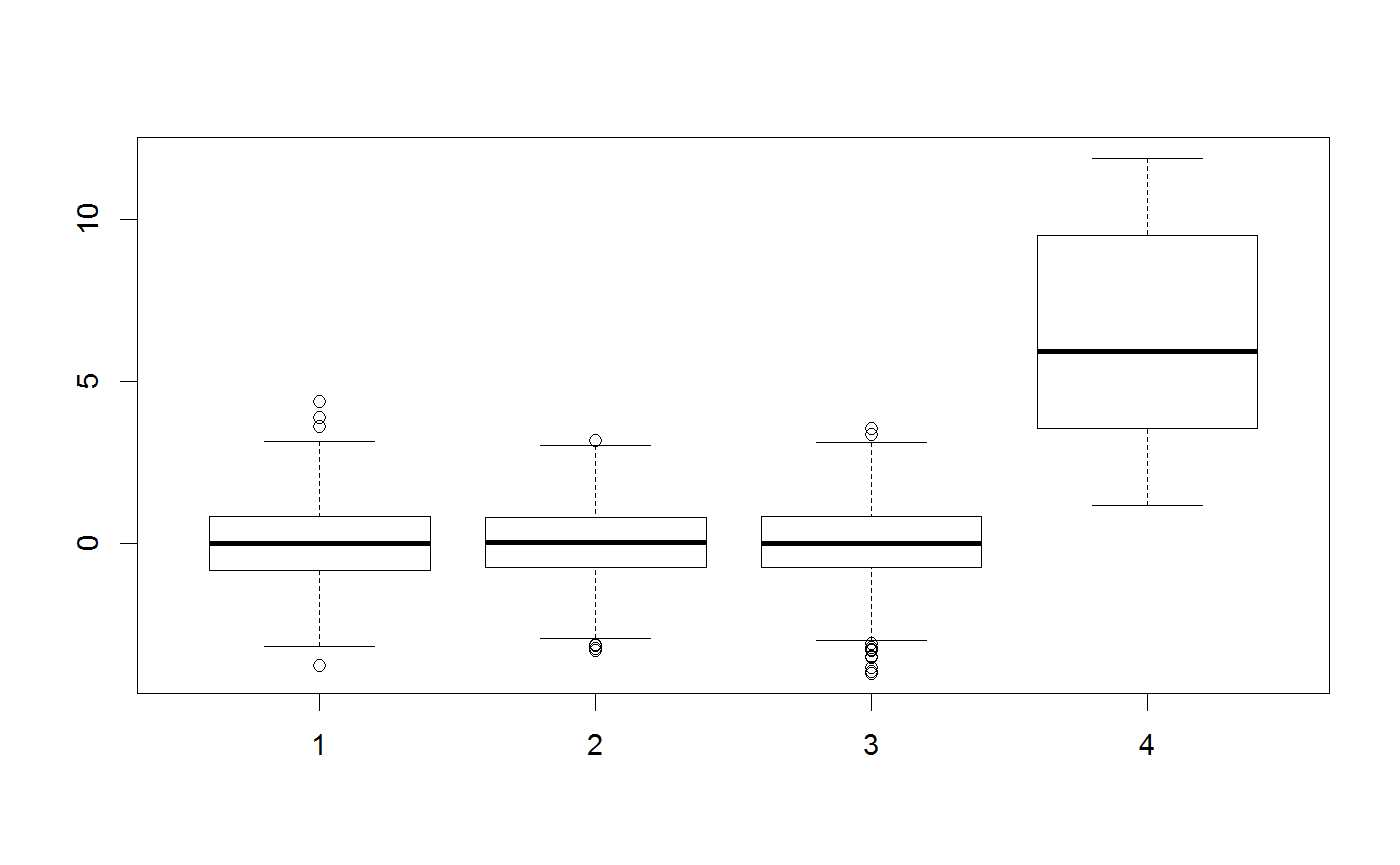Factory that creates a proposal generator

Factory that creates a proposal generator

createProposalGenerator(covariance, gibbsProbabilities = NULL,
  gibbsWeights = NULL, otherDistribution = NULL,
  otherDistributionLocation = NULL, otherDistributionScaled = F,
  message = F, method = "chol", scalingFactor = 2.38)

Arguments

covariance	covariance matrix. Can also be vector of the sqrt of diagonal elements --> standard deviation
gibbsProbabilities	optional probabilities for the number of parameters to vary in a Metropolis within gibbs style - for 4 parameters, c(1,1,0.5,0) means that at most 3 parameters will be varied, and it is double as likely to vary one or two than varying 3
gibbsWeights	optional probabilities for parameters to be varied in a Metropolis within gibbs style - default ist equal weight for all parameters - for 4 parameters, c(1,1,1,100) would mean that if 2 parameters would be selected, parameter 4 would be 100 times more likely to be picked than the others. If 4 is selected, the remaining parameters have equal probability.
otherDistribution	optional additinal distribution to be mixed with the default multivariate normal. The distribution needs to accept a parameter vector (to allow for the option of making the distribution dependend on the parameter values), but it is still assumed that the change from the current values is returned, not the new absolute values.
otherDistributionLocation	a vector with 0 and 1, denoting which parameters are modified by the otherDistribution
otherDistributionScaled	should the other distribution be scaled if gibbs updates are calculated?
message	print out parameter settings
method	method for covariance decomposition
scalingFactor	scaling factor for the proposals

See also

updateProposalGenerator

Examples

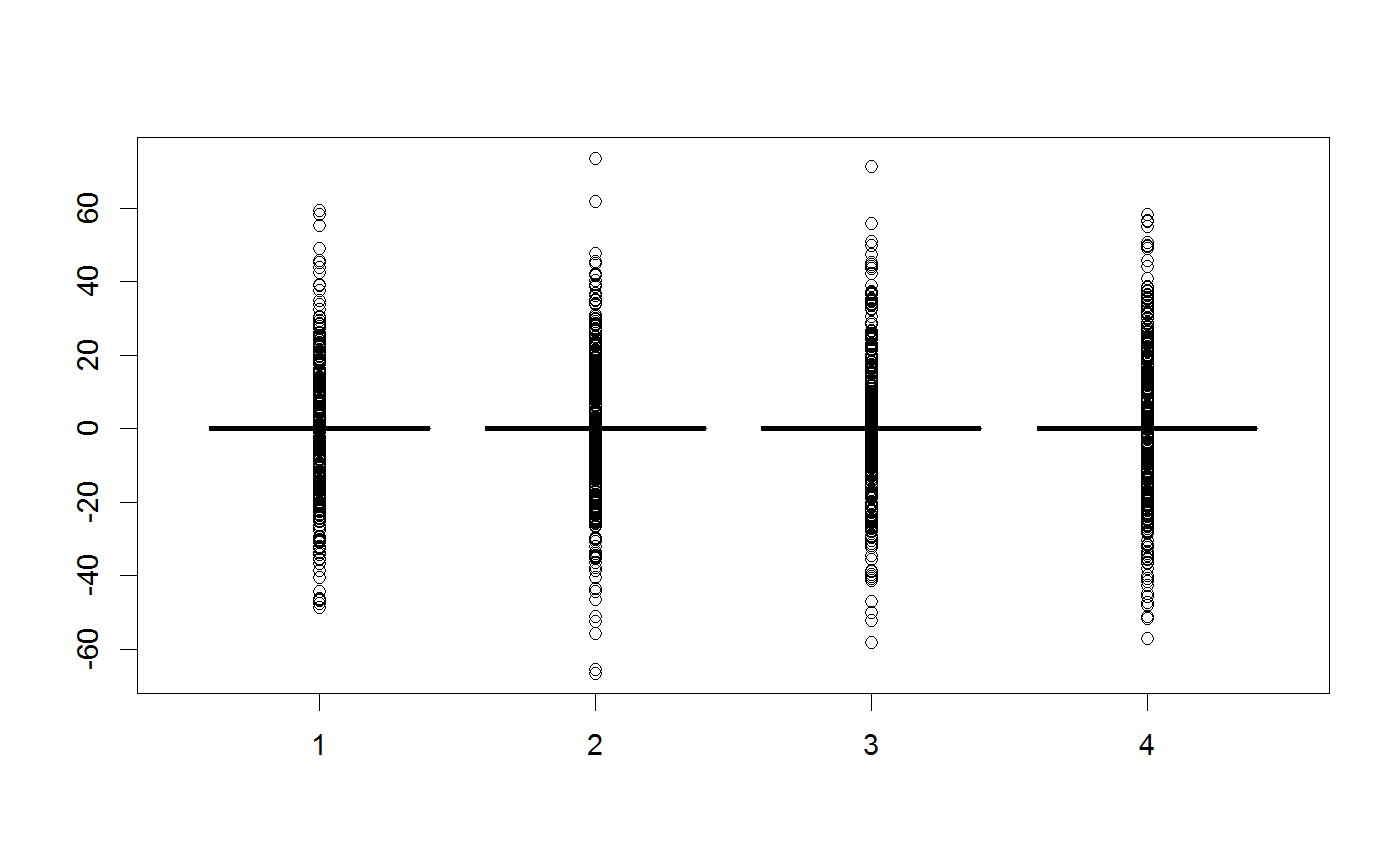
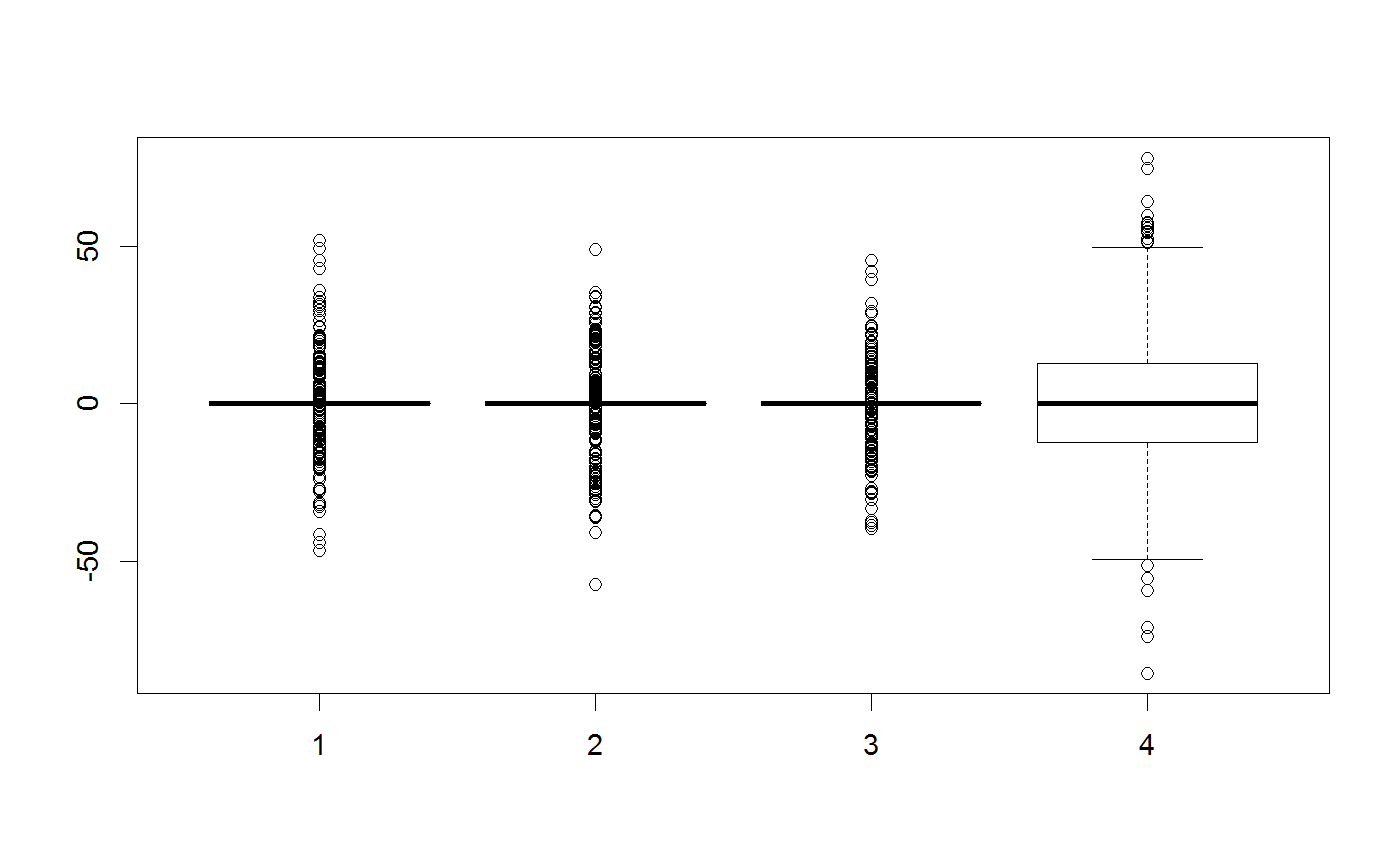
testMatrix = matrix(rep(c(0,0,0,0), 1000), ncol = 4)
testVector = c(0,0,0,0)


##Standard multivariate normal proposal generator

testGenerator <- createProposalGenerator(covariance = c(1,1,1,1), message = TRUE)
#> Proposalgenerator createdcovariance set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    0
#> [2,]    0    1    0    0
#> [3,]    0    0    1    0
#> [4,]    0    0    0    1
#> covarianceDecomp set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    0
#> [2,]    0    1    0    0
#> [3,]    0    0    1    0
#> [4,]    0    0    0    1
#> gibbsProbabilities set to:
#>  NULL
#> gibbsWeights set to:
#>  NULL
#> otherDistribution set to:
#>  NULL
#> otherDistributionLocation set to:
#>  NULL

methods(class = "proposalGenerator")
#> [1] print
#> see '?methods' for accessing help and source code
print(testGenerator)
#> covariance set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    0
#> [2,]    0    1    0    0
#> [3,]    0    0    1    0
#> [4,]    0    0    0    1
#> covarianceDecomp set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]    1    0    0    0
#> [2,]    0    1    0    0
#> [3,]    0    0    1    0
#> [4,]    0    0    0    1
#> gibbsProbabilities set to:
#>  NULL
#> gibbsWeights set to:
#>  NULL
#> otherDistribution set to:
#>  NULL
#> otherDistributionLocation set to:
#>  NULL

x = testGenerator$returnProposal(testVector)
x
#> [1] -0.08528815  0.96024687 -0.21403684  0.86855229

x <- testGenerator$returnProposalMatrix(testMatrix)
boxplot(x)

##Changing the covariance
testGenerator$covariance = diag(rep(100,4))
testGenerator <- testGenerator$updateProposalGenerator(testGenerator, message = TRUE)
#> Proposalgenerator settings changedcovariance set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]  100    0    0    0
#> [2,]    0  100    0    0
#> [3,]    0    0  100    0
#> [4,]    0    0    0  100
#> covarianceDecomp set to:
#>       [,1] [,2] [,3] [,4]
#> [1,]   10    0    0    0
#> [2,]    0   10    0    0
#> [3,]    0    0   10    0
#> [4,]    0    0    0   10
#> gibbsProbabilities set to:
#>  NULL
#> gibbsWeights set to:
#>  NULL
#> otherDistribution set to:
#>  NULL
#> otherDistributionLocation set to:
#>  NULL

testGenerator$returnProposal(testVector)
#> [1] -6.237000  2.271769  0.885039 -3.262444
x <- testGenerator$returnProposalMatrix(testMatrix)
boxplot(x)


##-Changing the gibbs probabilities / probability to modify 1-n parameters

testGenerator$gibbsProbabilities = c(1,1,0,0)
testGenerator <- testGenerator$updateProposalGenerator(testGenerator)

testGenerator$returnProposal(testVector)
#> [1] -27.17082   0.00000 -26.53460   0.00000
x <- testGenerator$returnProposalMatrix(testMatrix)
boxplot(x)


##-Changing the gibbs weights / probability to pick each parameter

testGenerator$gibbsWeights = c(0.3,0.3,0.3,100)
testGenerator <- testGenerator$updateProposalGenerator(testGenerator)

testGenerator$returnProposal(testVector)
#> [1] 11.78213  0.00000  0.00000 17.64915
x <- testGenerator$returnProposalMatrix(testMatrix)
boxplot(x)


##-Adding another function

otherFunction <- function(x) sample.int(10,1)

testGenerator <- createProposalGenerator(
  covariance = c(1,1,1),
  otherDistribution = otherFunction,
  otherDistributionLocation = c(0,0,0,1),
  otherDistributionScaled = TRUE
)

testGenerator$returnProposal(testVector)
#> [1]  0.7176416  1.8980108 -2.8475711  3.5700000
x <- testGenerator$returnProposalMatrix(testMatrix)
boxplot(x)
table(x[,4])
#> 
#>  1.19  2.38  3.57  4.76  5.95  7.14  8.33  9.52 10.71  11.9 
#>   129    92   113    97    96    87    89    99    98   100